Ортоцентър — точка на пресичане на височините на триъгълника

За да намерите ортоцентъра на триъгълника, можете да използвате калкулатора, където трябва да въведете координатите. В автоматичен режим изчисленията ще се извършват с помощта на формули. Можете също така да извършите всички изчисления ръчно.

Например, налични са следните данни:
A – 4,3;
В – 0,5;
С – 3,-6.
Първото, което трябва да се намери, е наклонът на страните, който е обозначен с - m , използвайки формулата:

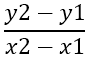
От това следва:

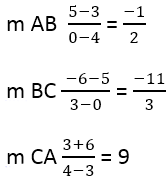
След това е необходимо да се намери наклонът на перпендикулярните страни, за това се използва формулата:

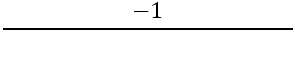
Имаме:
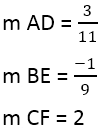Когато наклонът на перпендикулярите е намерен, можете да използвате уравнението на правите, например, за правата AD, където точката е 4,3, а наклонът е 3/11:

С помощта на опростяване имаме: 3x - 11y=-21
За правата VE, където точката е 0,5, а наклонът е -1/9, имаме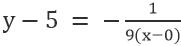

Опростяването дава: x+9y=45.
И последните прави CF, където точката е 3, -6, а наклонът е 2, имаме уравнението y+6 = 2(x-3).
И опростяване, 2x — y = 12.
Ако решите две от трите уравнения, ще бъдат намерени стойностите на x и y. За този пример:
Стойност на x = 8,05263;
Стойност на y = 4,10526.
Които в този случай са координатите на търсения Ортоцентър.