Ortocentro — punto de intersección de las alturas del triángulo

Para encontrar el ortocentro de un triángulo, puede usar el calculador donde debe ingresar las coordenadas. En modo automático, se realizarán cálculos utilizando fórmulas. También puede realizar todos los cálculos manualmente.

Por ejemplo, los siguientes puntos de datos están disponibles:
A – 4,3;
En – 0,5;
Con – 3,-6.
Lo primero que se debe encontrar es la pendiente de los lados, que se denota por - m , usando la fórmula:

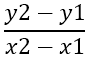
De esto se sigue:

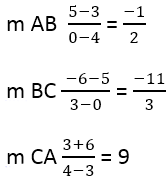
A continuación, es necesario encontrar la pendiente de los lados perpendiculares, para esto se usa la fórmula:

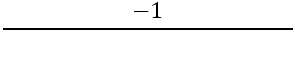
Tenemos:
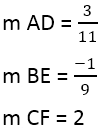Cuando se encuentra la pendiente de los perpendiculares, puede usar la ecuación de las líneas, por ejemplo, para la línea AD, donde el punto es 4,3, y la pendiente es 3/11:

Con la ayuda de la simplificación, tenemos: 3x - 11y=-21
Para la línea VE, donde el punto es 0,5, y la pendiente es -1/9, tenemos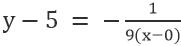

La simplificación da: x+9y=45.
Y las últimas líneas CF, donde el punto es 3, -6, y la pendiente es 2, tenemos la ecuación y+6 = 2(x-3).
Y simplificación, 2x — y = 12.
Si resuelve dos de las tres ecuaciones, se encontrarán los valores de x e y. Para este ejemplo:
Valor de x = 8,05263;
Valor de y = 4,10526.
Que en este caso son las coordenadas del ortocentro buscado.