Transposición de matrices

Una matriz transpuesta se obtiene reemplazando las filas de la matriz original por columnas o sus columnas por filas.

Propiedades de la transposición de matrices:
Una matriz transpuesta dos veces es igual a la matriz originalA^TT(A^T)^T=A
La matriz transpuesta de una suma es igual a la suma de las matrices transpuestas(A + B)^T=A^T+B^T
La matriz transpuesta de un producto es igual al producto de las matrices transpuestas de los factores, tomadas en orden inverso(A × B)^T=A^T×B^T

Para obtener una matriz transpuesta, necesita realizar una de las siguientes acciones con la matriz original:

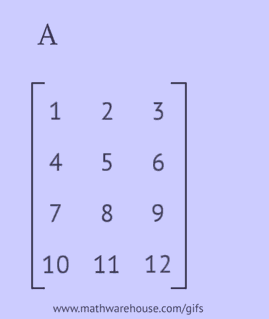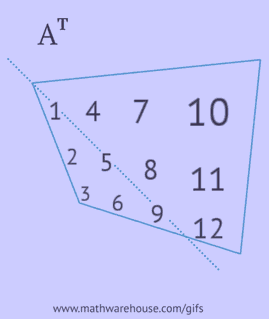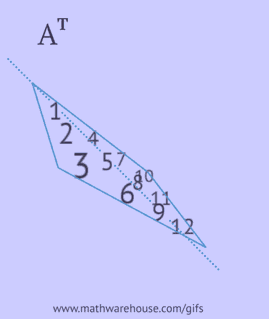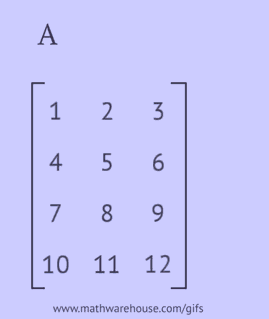
- escribir cada una de sus filas como una columna en el mismo orden;
- escribir cada una de sus columnas como una fila en el mismo orden;
- reflejar sus elementos respecto a la diagonal principal, comenzando desde la esquina superior izquierda y continuando a la derecha y hacia abajo hasta que se alcance el borde inferior o derecho.

Las matrices convertidas en transpuestas se utilizan para resolver sistemas de ecuaciones algebraicas, encontrar la matriz inversa, así como en otras tareas de álgebra lineal.