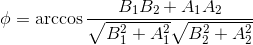Angle entre les lignes

Cette calculatrice est conçue pour calculer l'angle entre deux lignes en ligne.

Deux lignes peuvent avoir trois variantes de positionnement relatif l'une par rapport à l'autre. Elles peuvent coïncider, être parallèles ou se croiser. Pour déterminer l'angle entre les lignes, le cas le plus intéressant est l'angle entre les(ou se croiser) lignes.

Si deux lignes ont un point commun, ces lignes sont dites croiser. Le point d'intersection divise chacune des lignes en deux rayons. Entre les rayons des lignes croisées, quatre angles se forment (deux aigus et deux obtus). Ainsi, l'angle entre deux lignes croisées – est le plus petit angle (aigu), formé à l'intersection de ces lignes. Il convient de noter que si la valeur d'un des angles est connue, les valeurs des trois autres angles peuvent être facilement trouvées grâce aux propriétés des angles verticaux et adjacents.

Pour trouver l'angle entre deux lignes à l'aide de cette calculatrice, vous devez entrer les coefficients dans les équations des lignes et appuyer sur le bouton «Calculer».

Si les lignes sont données par les équations suivantes :

alors les vecteurs de direction de ces lignes seront égaux :

Nous utilisons la formule du produit scalaire de deux vecteurs :

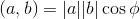
de cette formule nous obtiendrons :

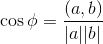
Exprimer l'angle φ :

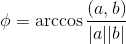
De la dernière formule, nous obtiendrons :