Orthocentre — point d'intersection des hauteurs du triangle

Pour trouver l'orthocentre d'un triangle, vous pouvez utiliser le calculateur où vous devez entrer les coordonnées. En mode automatique, les calculs seront effectués à l'aide de formules. Vous pouvez également effectuer tous les calculs manuellement.

Par exemple, les points de données suivants sont disponibles :
A – 4,3;
Dans – 0,5;
Avec – 3,-6.
La première chose à trouver est la pente des côtés, qui est notée par - m , en utilisant la formule :

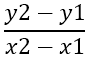
Il en résulte :

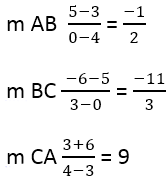
Ensuite, il est nécessaire de trouver la pente des côtés perpendiculaires, pour cela la formule est utilisée :

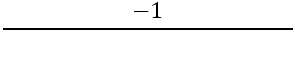
Nous avons :
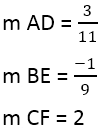Lorsque la pente des perpendiculaires est trouvée, vous pouvez utiliser l'équation des lignes, par exemple, pour la ligne AD, où le point est 4,3, et la pente est 3/11:

Avec l'aide de simplification, nous avons : 3x - 11y=-21
Pour la ligne VE, où le point est 0,5, et la pente est -1/9, nous avons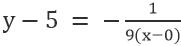

La simplification donne : x+9y=45.
Et les dernières lignes CF, où le point est 3, -6, et la pente est 2, nous avons l'équation y+6 = 2(x-3).
Et simplification, 2x — y = 12.
Si vous résolvez deux des trois équations, les valeurs de x et y seront trouvées. Pour cet exemple :
Valeur de x = 8,05263;
Valeur de y = 4,10526.
Qui, dans ce cas, sont les coordonnées de l'orthocentre recherché.