Ortocentro — punto di intersezione delle altezze del triangolo

Per trovare l'ortocentro di un triangolo, puoi utilizzare il calcolatore dove dovresti inserire le coordinate. In modalità automatica, i calcoli verranno eseguiti utilizzando le formule. Puoi anche eseguire tutti i calcoli manualmente.

Ad esempio, sono disponibili i seguenti punti dati:
A – 4,3;
In – 0,5;
Con – 3,-6.
La prima cosa da trovare è l'inclinazione dei lati, che è indicata da - m , usando la formula:

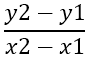
Da ciò segue:

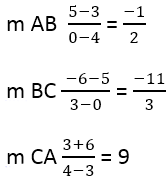
Successivamente, è necessario trovare l'inclinazione dei lati perpendicolari, per questo si utilizza la formula:

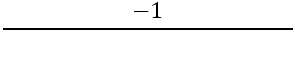
Abbiamo:
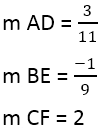Quando viene trovata l'inclinazione dei perpendicolari, puoi utilizzare l'equazione delle linee, ad esempio, per la linea AD, dove il punto è 4,3, e l'inclinazione è 3/11:

Con l'aiuto della semplificazione, abbiamo: 3x - 11y=-21
Per la linea VE, dove il punto è 0,5, e l'inclinazione è -1/9, abbiamo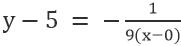

La semplificazione dà: x+9y=45.
E le ultime linee CF, dove il punto è 3, -6, e l'inclinazione è 2, abbiamo l'equazione y+6 = 2(x-3).
E la semplificazione, 2x — y = 12.
Se risolvi due delle tre equazioni, i valori di x e y verranno trovati. Per questo esempio:
Valore di x = 8,05263;
Valore di y = 4,10526.
Che in questo caso sono le coordinate dell'ortocentro cercato.