直交中心 — 三角形の高さの交点

三角形の直交中心を見つけるには、計算機を使用して座標を入力します。自動モードでは、計算は公式を使用して行われます。すべての計算を手動で行うこともできます。

例えば、次のデータポイントが利用可能です:
A – 4,3;
に – 0,5;
と– 3,-6.
最初に見つけるべきものは、辺の傾きであり、それは - で表されます m 、次の公式を使用して:

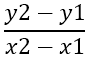
これから次のことがわかります:

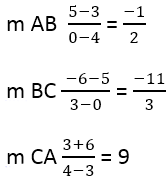
次に、垂直な辺の傾きを見つける必要があります。そのためには、次の公式を使用します:

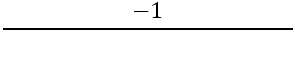
次があります:
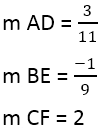垂直の傾きが見つかったら、線の方程式を使用できます。例えば、線 AD 、点が 4,3 で、傾きが 3 の場合/11:

簡略化を用いて、次のようになります: 3x - 11y=-21
線 VE の場合、点が 0,5 で、傾きが -1 の場合/9, 次があります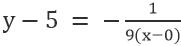

簡略化すると: x+9y=45.
そして最後の線 CF 、点が 3, -6 で、傾きが 2 の場合、次の方程式があります y+6 = 2(x-3).
そして簡略化、2x — y = 12.
3つの方程式のうち2つを解くと、xとyの値が得られます。この例では:
xの値 = 8,05263;
yの値 = 4,10526.
これらはこの場合、求める直交中心の座標です。