수심 — 삼각형 높이의 교차점

삼각형의 수심을 찾으려면 계산기를 사용하여 좌표를 입력하면 됩니다. 자동 모드에서 공식 사용을 통해 계산이 수행됩니다. 또한 모든 계산을 수동으로 수행할 수도 있습니다.

예를 들어, 다음 데이터 포인트가 있습니다:
A – 4,3;
에서 – 0,5;
와 함께 – 3,-6.
첫 번째로 찾아야 할 것은 변의 기울기이며, 이는 -로 표시됩니다 m , 공식을 사용하여:

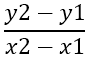
이로부터 다음이 따릅니다:

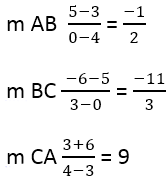
다음으로, 수직 변의 기울기를 찾아야 하며, 이를 위해 공식을 사용합니다:

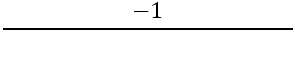
우리는 다음을 가지고 있습니다:
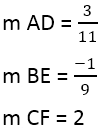수직선의 기울기를 찾았을 때, 선의 방정식을 사용할 수 있으며, 예를 들어, 선 AD, 점이 4,3이며 기울기가 3인 경우/11:

단순화를 통해, 우리는 다음을 가지고 있습니다: 3x - 11y=-21
선 VE의 경우, 점이 0,5이며 기울기가 -1인 경우/9, 우리는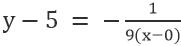

단순화는 다음을 제공합니다: x+9y=45.
그리고 마지막 라인들 CF, 점이 3, -6이며 기울기가 2인 경우, 우리는 방정식을 가지고 있습니다 y+6 = 2(x-3).
그리고 단순화, 2x — y = 12.
세 개의 방정식 중 두 개를 해결하면 x와 y의 값을 찾을 수 있습니다. 이 예제의 경우:
x 값 = 8,05263;
y 값 = 4,10526.
이는 이 경우에 찾고자 하는 수심의 좌표입니다.