Hoogtepunt — snijpunt van de hoogtelijnen van de driehoek

Om het hoogtepunt van een driehoek te vinden, kunt u de calculator gebruiken waarin u de coördinaten moet invoeren. In de automatische modus worden berekeningen uitgevoerd met behulp van formules. U kunt ook alle berekeningen handmatig uitvoeren.

Bijvoorbeeld, de volgende gegevenspunten zijn beschikbaar:
A – 4,3;
In – 0,5;
Met – 3,-6.
Het eerste dat moet worden gevonden, is de helling van de zijden, die wordt aangeduid met - m , met behulp van de formule:

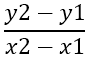
Hieruit volgt:

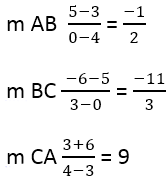
Vervolgens is het noodzakelijk om de helling van de loodrechte zijden te vinden, hiervoor wordt de formule gebruikt:

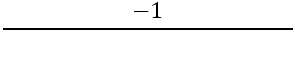
We hebben:
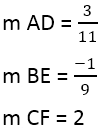Wanneer de helling van de loodlijnen is gevonden, kunt u de vergelijking van lijnen gebruiken, bijvoorbeeld voor de lijn AD, waar het punt 4,3 is, en de helling is 3/11:

Met behulp van vereenvoudiging hebben we: 3x - 11y=-21
Voor de lijn VE, waar het punt 0,5 is, en de helling is -1/9, we hebben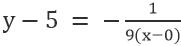

Vereenvoudiging geeft: x+9y=45.
En de laatste lijnen CF, waar het punt 3, -6 is, en de helling is 2, hebben we de vergelijking y+6 = 2(x-3).
En vereenvoudiging, 2x — y = 12.
Als u twee van de drie vergelijkingen oplost, worden de waarden van x en y gevonden. Voor dit voorbeeld:
Waarde van x = 8,05263;
Waarde van y = 4,10526.
Die in dit geval de coördinaten zijn van het gezochte hoogtepunt.