Root Mean Square Deviation
Root mean square deviation of two, three, four, and more numbers. It is also the standard deviation, root mean square deviation, root mean square, average quadratic, standard deviation — indicator of the dispersion of values of a random variable relative to its mathematical expectation in probability theory and statistics.
As a rule, the listed terms are equal to the square root of the variance.
Example of calculating the standard deviation using the following formulas:
Calculate the average grade of the student: 2; 4; 5; 6; 8.
Caverage grade will be equal to:
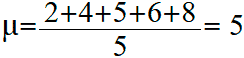
Calculate the squares of deviations of grades from their average grade:

Calculate the arithmetic mean (variance) of these values:
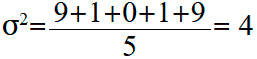
Standard deviation is equal to the square root of the variance:
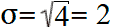
This formula is only valid if these five values are the general population. If these data were a random sample from a larger population (for example, the grades of five randomly selected students from a large city), then in the denominator of the formula for calculating the variance instead of n = 5 it would be necessary to put n − 1 = 4:
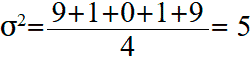
Then the standard deviation will be equal to:
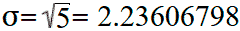
This result is called the standard deviation based on the unbiased estimate of variance. Division by n − 1 instead of n gives an unbiased estimate of the variance for large general populations.
Calculate the average grade of the student: 2; 4; 5; 6; 8.
Caverage grade will be equal to:
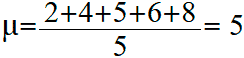
Calculate the squares of deviations of grades from their average grade:

Calculate the arithmetic mean (variance) of these values:
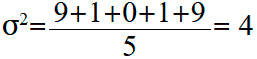
Standard deviation is equal to the square root of the variance:
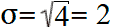
This formula is only valid if these five values are the general population. If these data were a random sample from a larger population (for example, the grades of five randomly selected students from a large city), then in the denominator of the formula for calculating the variance instead of n = 5 it would be necessary to put n − 1 = 4:
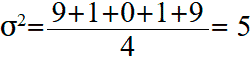
Then the standard deviation will be equal to:
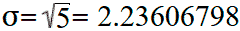
This result is called the standard deviation based on the unbiased estimate of variance. Division by n − 1 instead of n gives an unbiased estimate of the variance for large general populations.
