Pythagorean Theorem

The Pythagorean Theorem is a fundamental link in Euclidean geometry, on which a large part of all consequences and other theorems derived from the Pythagorean Theorem are based. It was derived in the VI century BC, the theorem relates the sides of a right triangle with a simple equation, and it has many proofs, one of which combines both algebra and geometry.

According to the Pythagorean theorem, in a right triangle, there are legs a and b – these are the sides adjacent to the right angle, and the sum of their squares gives the square of the hypotenuse – the third side of the triangle, opposite the right angle.

This can be proved by constructing four right triangles so that the long leg of each of them is the short leg of the next triangle, with the vertices of the angles coinciding.

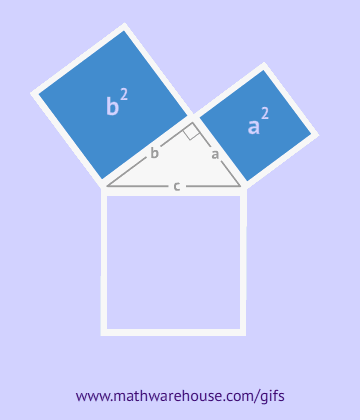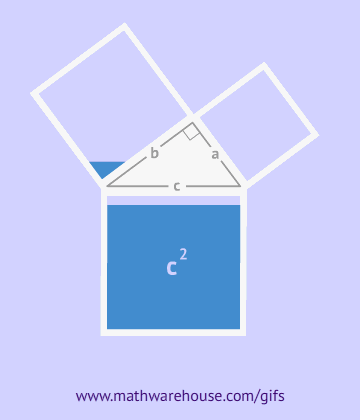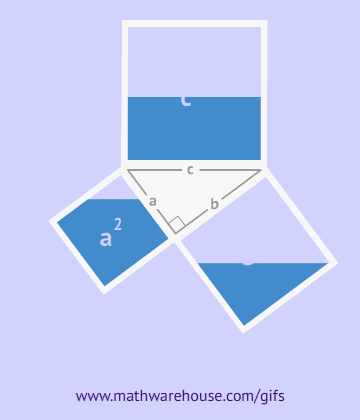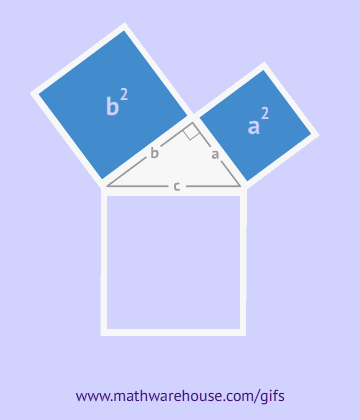
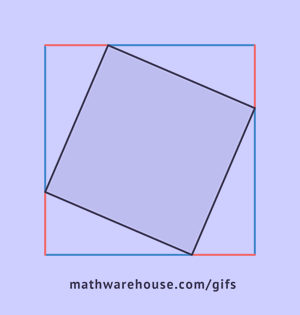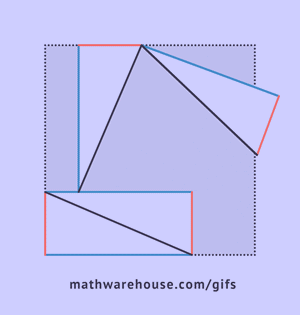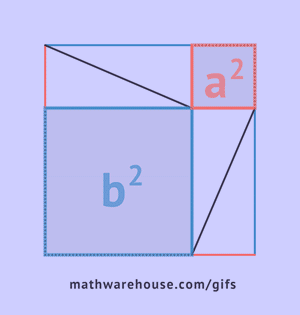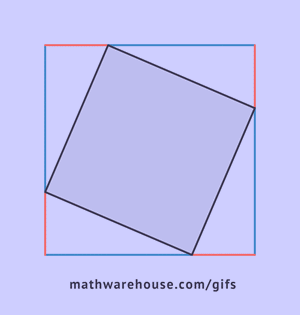
As can be seen from the drawing, the overall figure represents a square with a side c, simultaneously being the hypotenuse of these triangles, and the area of this figure is equal to c², according to the formula for the area of a square. In addition to this square, it includes four right triangles with an area of , in the center of it there is another small square. The side of the small square is equal to the difference of the legs, therefore, its area will be equal to the square of this difference. (a-b)²=a²-2ab+b²

Let's represent the area of the large square as the sum of the areas of the small square and four triangles according to the principle of superposition.

Thus, the area of the square is simultaneously equal to the hypotenuse squared and the sum of the squares of the legs, which was to be proven. a²+b²=c²