• Wszystkie kalkulatory
    • /
  • Edukacja i nauka
    • /
  • Matematyka
    • /   Ortocentrum — punkt przecięcia wysokości trójkąta

    Ortocentrum — punkt przecięcia wysokości trójkąta

    Aby znaleźć ortocentrum trójkąta, możesz skorzystać z kalkulatora, w którym powinieneś wprowadzić współrzędne. W trybie automatycznym obliczenia zostaną przeprowadzone za pomocą wzorów. Możesz również przeprowadzić wszystkie obliczenia ręcznie.

    Kropka Współrzędne X Współrzędne Y
    A
    B
    C
    Ortocentrum Trójkąta

    Na przykład, dostępne są następujące dane:
    A – 4,3;
    W – 0,5;
    Z – 3,-6.
     Pierwszą rzeczą do znalezienia jest nachylenie boków, które oznaczamy jako - m , używając wzoru:

    Wzór na ortocentrum—punkt przecięcia wysokości trójkąta

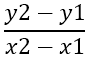
    Z tego wynika:
    Wzór na ortocentrum—punkt przecięcia wysokości trójkąta

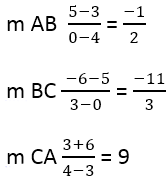
    Następnie należy znaleźć nachylenie prostopadłych boków, do tego używamy wzoru:

    Wzór na ortocentrum—punkt przecięcia wysokości trójkąta

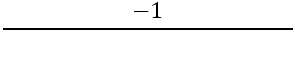
    Mamy:
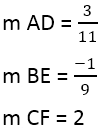    Wzór na ortocentrum—punkt przecięcia wysokości trójkąta Gdy nachylenie prostopadłych boków zostanie znalezione, można użyć równania prostych, na przykład dla linii AD, gdzie punkt to 4,3, a nachylenie to 3/11:

    y-y1 = m(x-x1) y-3 = 3/11(x-4)

    Za pomocą uproszczenia mamy: 3x - 11y=-21
    Dla linii VE, gdzie punkt to 0,5, a nachylenie to -1/9, mamy 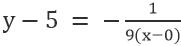Wzór na ortocentrum—punkt przecięcia wysokości trójkąta

    Uproszczenie daje: x+9y=45.
    I ostatnie linie CF, gdzie punkt to 3, -6, a nachylenie to 2, mamy równanie y+6 = 2(x-3).
    I uproszczenie, 2x — y = 12.
    Jeśli rozwiążesz dwa z trzech równań, wartości x i y zostaną znalezione. Dla tego przykładu:
    Wartość x = 8,05263;
    Wartość y = 4,10526.
    Które w tym przypadku są współrzędnymi poszukiwanego Ortocentrum.