Ortocentro — ponto de interseção das alturas do triângulo

Para encontrar o ortocentro de um triângulo, pode usar a calculadora onde deve inserir as coordenadas. Em modo automático, os cálculos serão realizados utilizando fórmulas. Também pode realizar todos os cálculos manualmente.

Por exemplo, os seguintes pontos de dados estão disponíveis:
A – 4,3;
Em – 0,5;
Com – 3,-6.
A primeira coisa a encontrar é a inclinação dos lados, que é denotada por - m , usando a fórmula:

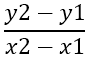
Disso se segue:

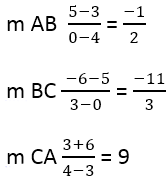
Em seguida, é necessário encontrar a inclinação dos lados perpendiculares, para isso utiliza-se a fórmula:

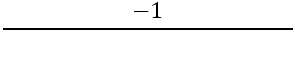
Temos:
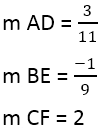Quando a inclinação dos perpendiculares é encontrada, pode utilizar a equação das linhas, por exemplo, para a linha AD, onde o ponto é 4,3, e a inclinação é 3/11:

Com a ajuda da simplificação, temos: 3x - 11y=-21
Para a linha VE, onde o ponto é 0,5, e a inclinação é -1/9, temos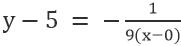

A simplificação dá: x+9y=45.
E as últimas linhas CF, onde o ponto é 3, -6, e a inclinação é 2, temos a equação y+6 = 2(x-3).
E simplificação, 2x — y = 12.
Se resolver duas das três equações, os valores de x e y serão encontrados. Para este exemplo:
Valor de x = 8,05263;
Valor de y = 4,10526.
Que neste caso são as coordenadas do ortocentro procurado.