Ortocentru — punctul de intersecție al înălțimilor triunghiului

Pentru a găsi ortocentrul unui triunghi, puteți folosi calculatorul unde trebuie să introduceți coordonatele. În modul automat, calculele vor fi efectuate folosind formule. De asemenea, puteți efectua toate calculele manual.

De exemplu, următoarele puncte de date sunt disponibile:
A – 4,3;
În – 0,5;
Cu – 3,-6.
Primul lucru de găsit este panta laturilor, care este notată cu - m , folosind formula:

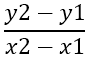
Din acest lucru rezultă:

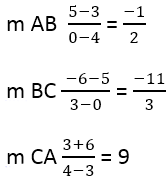
În continuare, este necesar să se găsească panta laturilor perpendiculare, pentru aceasta se folosește formula:

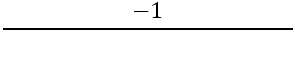
Avem:
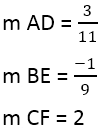Când panta perpendicularilor este găsită, puteți folosi ecuația liniilor, de exemplu, pentru linia AD, unde punctul este 4,3, iar panta este 3/11:

Cu ajutorul simplificării, avem: 3x - 11y=-21
Pentru linia VE, unde punctul este 0,5, iar panta este -1/9, avem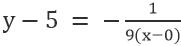

Simplificarea dă: x+9y=45.
Și ultimele linii CF, unde punctul este 3, -6, iar panta este 2, avem ecuația y+6 = 2(x-3).
Și simplificare, 2x — y = 12.
Dacă rezolvați două din cele trei ecuații, valorile x și y vor fi găsite. Pentru acest exemplu:
Valoarea x = 8,05263;
Valoarea y = 4,10526.
Care în acest caz sunt coordonatele ortocentrului căutat.