Ortocenter — presečišče višin trikotnika

Da bi našli ortocenter trikotnika, lahko uporabite kalkulator, kjer morate vnesti koordinate. V samodejnem načinu bodo izračuni izvedeni s pomočjo formul. Vse izračune lahko izvedete tudi ročno.

Na primer, na voljo so naslednje točke podatkov:
A – 4,3;
V – 0,5;
S – 3,-6.
Prva stvar, ki jo je treba najti, je naklon stranic, ki je označen z - m , s pomočjo formule:

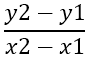
Iz tega sledi:

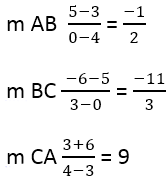
Nato je treba najti naklon pravokotnih stranic, za kar se uporabi formula:

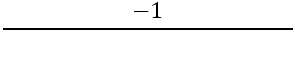
Imamo:
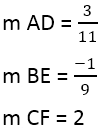Ko je naklon pravokotnic najden, lahko uporabite enačbo premic, na primer za premico AD, kjer je točka 4,3, in naklon je 3/11:

S pomočjo poenostavitve imamo: 3x - 11y=-21
Za premico VE, kjer je točka 0,5, in naklon je -1/9, imamo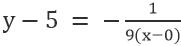

Poenostavitev daje: x+9y=45.
In zadnje premice CF, kjer je točka 3, -6, in naklon je 2, imamo enačbo y+6 = 2(x-3).
In poenostavitev, 2x — y = 12.
Če rešite dve od treh enačb, bodo najdene vrednosti x in y. Za ta primer:
Vrednost x = 8,05263;
Vrednost y = 4,10526.
Kar v tem primeru predstavljajo koordinate iskanega ortocentra.