Ortocentar — tačka preseka visina trougla

Da biste pronašli ortocentar trougla, možete koristiti kalkulator gde bi trebalo uneti koordinate. U automatskom režimu, izračunavanja će biti izvršena pomoću formula. Takođe možete izvršiti sva izračunavanja ručno.

Na primer, dostupne su sledeće tačke podataka:
A – 4,3;
U – 0,5;
Sa – 3,-6.
Prvo što treba pronaći je nagib stranica, koji je označen sa - m , koristeći formulu:

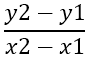
Iz ovoga sledi:

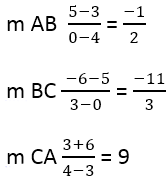
Dalje, potrebno je pronaći nagib normalnih stranica, za to se koristi formula:

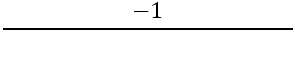
Imamo:
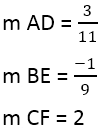Kada je nagib normalnih pronađen, možete koristiti jednačinu pravaca, na primer, za pravac AD, gde je tačka 4,3, a nagib je 3/11:

Uz pomoć pojednostavljenja, imamo: 3x - 11y=-21
Za pravac VE, gde je tačka 0,5, a nagib je -1/9, imamo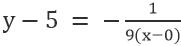

Pojednostavljenje daje: x+9y=45.
I poslednji pravci CF, gde je tačka 3, -6, a nagib je 2, imamo jednačinu y+6 = 2(x-3).
I pojednostavljenje, 2x — y = 12.
Ako rešite dve od tri jednačine, vrednosti x i y će biti pronađene. Za ovaj primer:
Vrednost x = 8,05263;
Vrednost y = 4,10526.
Koje u ovom slučaju predstavljaju koordinate traženog ortocentra.