Ортоцентр — точка перетину висот трикутника

Щоб знайти ортоцентр трикутника, ви можете скористатися калькулятором, де потрібно ввести координати. В автоматичному режимі обчислення виконуватимуться за допомогою формул. Ви також можете виконати всі обчислення вручну.

Наприклад, доступні такі точки даних:
A – 4,3;
У – 0,5;
З – 3,-6.
Перше, що потрібно знайти, це нахил сторін, який позначається як - m , використовуючи формулу:

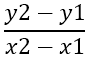
З цього випливає:

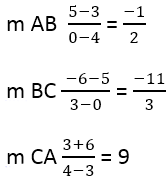
Далі необхідно знайти нахил перпендикулярних сторін, для цього використовується формула:

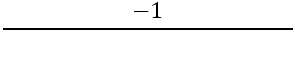
Маємо:
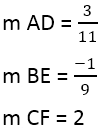Коли нахил перпендикулярів знайдено, можна використовувати рівняння прямих, наприклад, для прямої AD, де точка 4,3, а нахил 3/11:

За допомогою спрощення маємо: 3x - 11y=-21
Для прямої VE, де точка 0,5, а нахил -1/9, маємо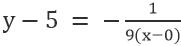

Спрощення дає: x+9y=45.
І останні лінії CF, де точка 3, -6, а нахил 2, маємо рівняння y+6 = 2(x-3).
І спрощення, 2x — y = 12.
Якщо вирішити два з трьох рівнянь, будуть знайдені значення x та y. У цьому прикладі:
Значення x = 8,05263;
Значення y = 4,10526.
Які в даному випадку є координатами шуканого Ортоцентра.