Trực tâm — điểm giao của các đường cao của tam giác

Để tìm trực tâm của một tam giác, bạn có thể sử dụng máy tính nơi bạn nên nhập các tọa độ. Ở chế độ tự động, các phép tính sẽ được thực hiện bằng cách sử dụng các công thức. Bạn cũng có thể thực hiện tất cả các phép tính thủ công.

Ví dụ, các điểm dữ liệu sau có sẵn:
A – 4,3;
Trong – 0,5;
Với – 3,-6.
Điều đầu tiên cần tìm là độ dốc của các cạnh, được ký hiệu là - m , sử dụng công thức:

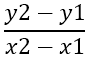
Từ điều này suy ra:

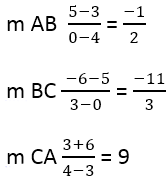
Tiếp theo, cần phải tìm độ dốc của các cạnh vuông góc, để làm điều này, công thức được sử dụng:

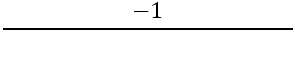
Chúng ta có:
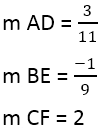Khi độ dốc của các đường vuông góc được tìm thấy, bạn có thể sử dụng phương trình của các đường thẳng, ví dụ, cho đường thẳng AD, nơi điểm là 4,3, và độ dốc là 3/11:

Với sự giúp đỡ của đơn giản hóa, chúng ta có: 3x - 11y=-21
Cho đường thẳng VE, nơi điểm là 0,5, và độ dốc là -1/9, chúng ta có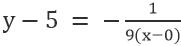

Đơn giản hóa cho: x+9y=45.
Và các đường thẳng cuối cùng CF, nơi điểm là 3, -6, và độ dốc là 2, chúng ta có phương trình y+6 = 2(x-3).
Và đơn giản hóa, 2x — y = 12.
Nếu bạn giải hai trong số ba phương trình, các giá trị x và y sẽ được tìm thấy. Cho ví dụ này:
Giá trị của x = 8,05263;
Giá trị của y = 4,10526.
Cái mà trong trường hợp này là tọa độ của trực tâm được tìm kiếm.