Ortocenter — skæringspunktet for højderne af trekanten

For at finde ortocenteret af en trekant kan du bruge kalkulatoren, hvor du skal indtaste koordinaterne. I automatisk tilstand vil beregninger blive udført ved hjælp af formler. Du kan også udføre alle beregninger manuelt.

For eksempel er følgende datapunkter tilgængelige:
A – 4,3;
I – 0,5;
Med – 3,-6.
Det første, der skal findes, er hældningen af siderne, som er angivet med - m , ved hjælp af formlen:

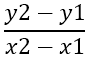
Heraf følger:

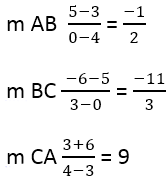
Dernæst er det nødvendigt at finde hældningen af de vinkelrette sider, til dette bruges formlen:

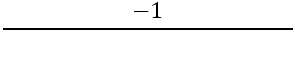
Vi har:
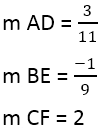Når hældningen af de vinkelrette er fundet, kan du bruge linjens ligning, for eksempel, for linjen AD, hvor punktet er 4,3, og hældningen er 3/11:

Med hjælp af forenkling har vi: 3x - 11y=-21
For linjen VE, hvor punktet er 0,5, og hældningen er -1/9, har vi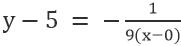

Forenkling giver: x+9y=45.
Og de sidste linjer CF, hvor punktet er 3, -6, og hældningen er 2, har vi ligningen y+6 = 2(x-3).
Og forenkling, 2x — y = 12.
Hvis du løser to af de tre ligninger, vil værdierne af x og y blive fundet. For dette eksempel:
Værdi af x = 8,05263;
Værdi af y = 4,10526.
Som i dette tilfælde er koordinaterne for det søgte Ortocenter.