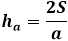Altura del Triángulo

En un triángulo arbitrario (donde todos los lados tienen longitudes diferentes), las alturas trazadas a los lados , medianas y bisectrices representan líneas completamente diferentes. Para encontrar la altura en un triángulo, no se pueden usar las propiedades de la mediana o la bisectriz como en los triángulos isósceles o equiláteros, por lo que deben usarse otros métodos.

Uno de los métodos similares implica usar un parámetro común del triángulo - el área. El algoritmo de cálculo se basa en el hecho de que el área de un triángulo escaleno se puede encontrar de varias maneras, incluidas a través de la altura. Conociendo los tres lados del triángulo, puedes encontrar su área usando la fórmula de Herón, y luego, usando otra fórmula de área, expresar la altura a través de ella.

Para calcular el área de un triángulo usando la fórmula de Herón, primero debes calcular el semiperímetro del triángulo. Como su nombre indica, el semiperímetro es el perímetro, o la suma de las longitudes de los tres lados, dividido por dos.

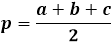
La fórmula del área en sí es el producto del semiperímetro con su diferencia de cada lado, estando toda la expresión bajo la raíz cuadrada.

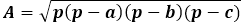
Por otro lado, la misma área del triángulo a través de la altura equivale a la mitad del producto del lado del triángulo con la altura trazada a él. Así, la altura es igual al doble del área dividido por el lado del triángulo. De la fórmula anterior, puedes expresar el área a través de los tres lados del triángulo y sustituirlo en la fórmula de la altura.

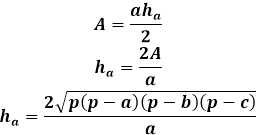
Esta fórmula de altura a través de los lados del triángulo es aplicable para cualquier triángulo, escaleno, isósceles o equilátero, en ausencia de otros.

Calcular la altura de un triángulo conociendo los tres lados requiere un largo camino usando fórmulas de área. La altura del triángulo expresada a través del área solo está relacionada con el lado al que se traza, por lo que es extremadamente importante indicar adecuadamente el orden de los lados para la calculadora y en el cálculo manual para sustituir el lado apropiado en la fórmula de la altura.

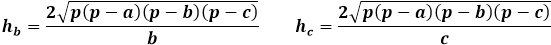
Fórmula de la altura de un triángulo arbitrario a través del área