Ortosentri — kolmion korkeuksien leikkauspiste

Kolmion ortosentrin löytämiseksi voit käyttää laskinta, johon sinun on syötettävä koordinaatit. Automaattisessa tilassa laskelmat suoritetaan kaavojen avulla. Voit myös suorittaa kaikki laskelmat manuaalisesti.

Esimerkiksi seuraavat tietopisteet ovat saatavilla:
A – 4,3;
In – 0,5;
Kanssa – 3,-6.
Ensimmäinen asia, joka on löydettävä, on sivujen kaltevuus, joka merkitään - m , käytetään kaavaa:

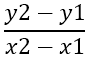
Tästä seuraa:

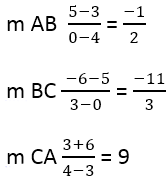
Seuraavaksi on löydettävä kohtisuorien sivujen kaltevuus, käytetään tätä kaavaa:

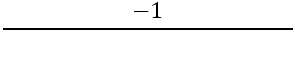
Meillä on:
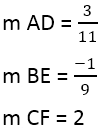Kun kohtisuorien kaltevuudet on löydetty, voit käyttää suorien yhtälöitä, esimerkiksi suoralle AD, jossa piste on 4,3, ja kaltevuus on 3/11:

Yksinkertaistamisen avulla saamme: 3x - 11y=-21
Suoralle VE, jossa piste on 0,5, ja kaltevuus on -1/9, meillä on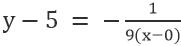

Yksinkertaistaminen antaa: x+9y=45.
Ja viimeiset suorat CF, jossa piste on 3, -6, ja kaltevuus on 2, meillä on yhtälö y+6 = 2(x-3).
Ja yksinkertaistaminen, 2x — y = 12.
Jos ratkaiset kaksi kolmesta yhtälöstä, löydät x:n ja y:n arvot. Tässä esimerkissä:
Arvo x = 8,05263;
Arvo y = 4,10526.
Jotka tässä tapauksessa ovat etsityn ortosentroidin koordinaatit.