Daļu saskaitīšana
Daļu saskaitīšana ar vienādiem saucējiem:
Definīcija: Daļu summa ar vienādiem saucējiem ir daļa, kuras skaitītājs ir vienāds ar sākotnējo daļu skaitītāju summu, un saucējs ir vienāds ar abu daļu saucēju.Formula
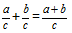
Saskaitīsim divas daļas ar vienādiem saucējiem
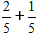
Saskaņā ar formulu mēs saskaitām skaitītājus un saglabājam saucēju tādu pašu
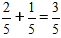
Svarīgi: Ja iespējams, mēs rakstām vienkāršotu daļu galīgajā atbildē.
Piemērs:
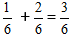Vienkāršojot daļu, mēs iegūstam skaitli 1/2 Daļu saskaitīšana ar dažādiem saucējiem:
Definīcija: Lai atrastu daļu summu ar dažādiem saucējiem, vispirms pārvediet daļas uz kopīgu saucēju, un pēc tam saskaitiet tās kā daļas ar vienādiem saucējiem.Uzdevums:
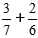
Risinājuma gaita:
1) Mēs pārvedam daļas uz kopīgu saucēju.
Lai to izdarītu, mēs atrodam LKD - Lielākais Kopīgais Dalītājs, priekš saucējiem 7 un 6, šis skaitlis ir 42.
Dalām skaitli 42 ar daļu saucējiem 3/7 un 2/6
Tādējādi, mēs atradām papildus reizinātājus.
Nākamais, reizinām daļas ar papildus reizinātājiem un iegūstam izteiksmi:
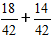
2) Saskaitām daļas.
Mūsu gadījumā, daļu var vienkāršot ar 2, un galīgajā atbildē mēs rakstām skaitli 16/21
Daļas un vesela skaitļa saskaitīšana:
Definīcija: Lai saskaitītu daļu ar veselu skaitli, vispirms pārstāvējam veselo skaitli kā daļu ar saucēju, kas ir vienāds ar 1.Aprēķina algoritms:
1) Mēs pārvedam daļas uz kopīgu saucēju.
2) Saskaitām daļas
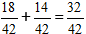
3) Ja iespējams, vienkāršojam iegūto daļu.
4) Ja rezultāts ir neīsta daļa, aprēķinām no tās veselo daļu.
Piemērs:
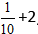
Risinājums:
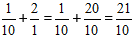
Aprēķinām veselo daļu un iegūstam atbildi
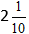
Jaukto daļu saskaitīšana:
Definīcija: Lai saskaitītu jauktās daļas nepieciešams atsevišķi saskaitīt veselos un daļējos skaitļus.Formula
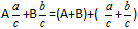
Piemērs:
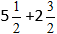
Ievietojam skaitļus formulā:
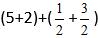
Mēs iegūstam:
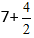
No daļas aprēķinām veselo daļu, jo tā ir neīsta, un iegūstam izteiksmi 7+2=9.