Ortocentrs — trijstūra augstumu krustpunktā

Lai atrastu trijstūra ortocentru, varat izmantot kalkulatoru, kurā jāievada koordinātas. Automātiskajā režīmā aprēķini tiks veikti, izmantojot formulas. Jūs varat arī veikt visus aprēķinus manuāli.

Piemēram, ir pieejami šādi dati:
A – 4,3;
In – 0,5;
Ar – 3,-6.
Pirmais, kas jāatrod, ir malu slīpums, kas tiek apzīmēts ar - m , izmantojot formulu:

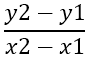
No tā izriet:

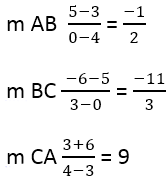
Tālāk ir nepieciešams atrast perpendikulāro malu slīpumu, tam tiek izmantota formula:

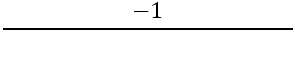
Mums ir:
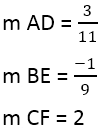Kad perpendikulu slīpums ir atrasts, jūs varat izmantot taisņu vienādojumus, piemēram, taisnei AD, kur punkts ir 4,3, un slīpums ir 3/11:

Ar vienkāršošanas palīdzību, mums ir: 3x - 11y=-21
Taisnei VE, kur punkts ir 0,5, un slīpums ir -1/9, mums ir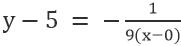

Vienkāršošana dod: x+9y=45.
Un pēdējās taisnes CF, kur punkts ir 3, -6, un slīpums ir 2, mums ir vienādojums y+6 = 2(x-3).
Un vienkāršošana, 2x — y = 12.
Ja atrisināsiet divus no trim vienādojumiem, tiks atrastas x un y vērtības. Šim piemēram:
x vērtība = 8,05263;
y vērtība = 4,10526.
Kas šajā gadījumā ir meklētā ortocentra koordinātas.