Matrisetransposisjon

En transponert matrise oppnås ved å erstatte radene i den opprinnelige matrisen med kolonner eller dens kolonner med rader.

Egenskaper ved matrisetransposisjon:
En matrise transponert to ganger er lik den opprinnelige matrisen A^TT(A^T)^T=A
Den transponerte matrisen av en sum er lik summen av de transponerte matriser (A + B)^T=A^T+B^T
Den transponerte matrisen av et produkt er lik produktet av de transponerte matrisene av faktorene, tatt i omvendt rekkefølge (A × B)^T=A^T×B^T

For å oppnå en transponert matrise, må du utføre en av følgende handlinger med den opprinnelige matrisen:

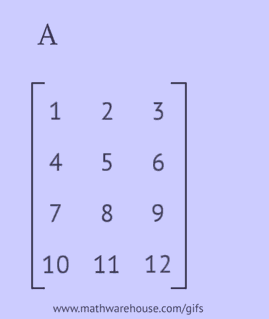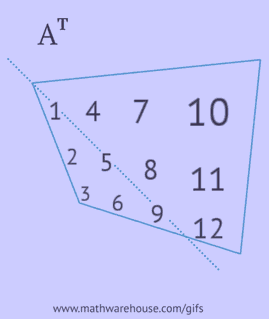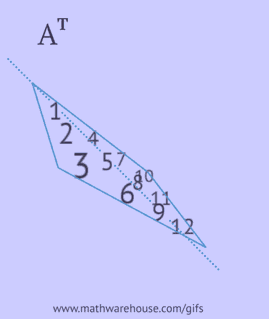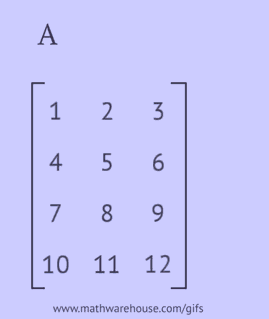
- skriv hver av dens rader som en kolonne i samme rekkefølge;
- skriv hver av dens kolonner som en rad i samme rekkefølge;
- reflektere dens elementer i forhold til hoveddiagonalen, starter fra det øvre venstre hjørnet og fortsetter til høyre og ned til nedre eller høyre kant er nådd.

Matriser konvertert til transponerte brukes for løsning av systemer av algebraiske ligninger, finne den inverse matrisa, samt i andre oppgaver i lineær algebra.