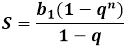Sum of geometric progression

The sum of a geometric progression has several different representations, which depend on the ratio of the progression. For an increasing positive, negative, or alternating progression, only the sum of the first few terms of the geometric progression is valid, the number of which must be limited, as the sequence itself will be infinite.

For a progression whose ratio is between zero and one, that is, a proper fraction (0<to<1), the sum of the entire sequence will be a quite unequivocal specific number, as the entire numeric series will be decreasing. The sum of the infinitely decreasing geometric progression has its separate formula, which can be found in the corresponding section, along with the calculator.

To find the sum of the first terms of a geometric progression, it is necessary to know the first term and the ratio of the progression. If any other term of the progression is given in the problem conditions, besides the first, then you will need to first use the formula of the first term of the geometric progression to calculate it, and substitute the obtained value in the online sum calculator.

Formula for the sum of the first three, four, or n terms of a geometric progression is derived using the geometric mean, as the main property of this progression. Any of the numbers in the series will be equal to the geometric mean of its neighbors:

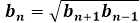
If you combine this property with the ratio of two consecutive terms of the progression, which is invariably equal to the same number - the ratio, then by simple reductions, the sum of the first few terms of the geometric progression is reduced to this form:

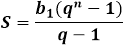
In some sources, a similar version is found, but with different signs in brackets - essentially this does not change the final value, and for manual calculation, when the first few terms are given, it is appropriate to use the most convenient formula at the moment.