Matrix transposition

A transposed matrix is obtained by replacing the rows of the original matrix with columns or its columns with rows.

Properties of matrix transposition:
A matrix transposed twice is equal to the original matrix A^TT(A^T)^T=A
The transposed matrix of a sum is equal to the sum of the transposed matrices (A + B)^T=A^T+B^T
The transposed matrix of a product is equal to the product of the transposed matrices of the factors, taken in reverse order (A × B)^T=A^T×B^T

To obtain a transposed matrix, you need to perform one of the following actions with the original matrix:

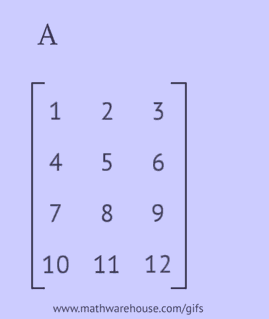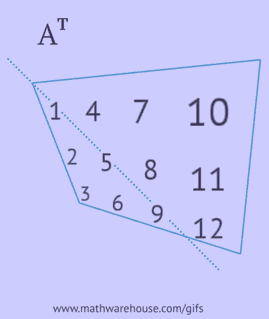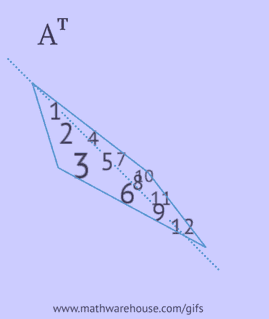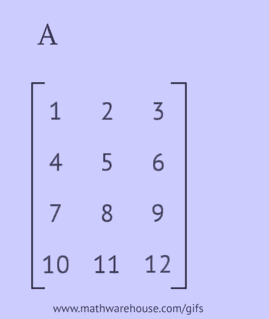
- write each of its rows as a column in the same order;
- write each of its columns as a row in the same order;
- reflect its elements relative to the main diagonal, starting from the upper left corner and continuing to the right and down until the lower or right edge is reached.

Matrices converted to transposed ones are used for solving systems of algebraic equations, finding the inverse matrix, as well as in other tasks of linear algebra.