Ortcentrum — skärningspunkt för triangelns höjder

För att hitta ortocentret i en triangel kan du använda kalkylatorn där du ska ange koordinaterna. I automatiskt läge kommer beräkningar att utföras med hjälp av formler. Du kan också utföra alla beräkningar manuellt.

Exempelvis finns följande datapunkter tillgängliga:
A – 4,3;
I – 0,5;
Med – 3,-6.
Det första att hitta är lutningen av sidorna, som betecknas med - m , med hjälp av formeln:

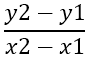
Av detta följer:

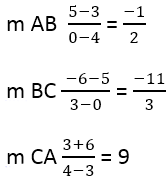
Nästa steg är att hitta lutningen för de vinkelräta sidorna, för detta används formeln:

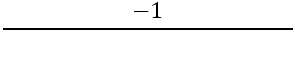
Vi har:
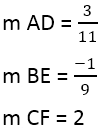När lutningen för de vinkelräta är funnen kan du använda ekvationen för linjer, till exempel för linjen AD, där punkten är 4,3, och lutningen är 3/11:

Med hjälp av förenkling har vi: 3x - 11y=-21
För linjen VE, där punkten är 0,5, och lutningen är -1/9, har vi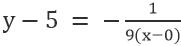

Förenkling ger: x+9y=45.
Och de sista linjerna CF, där punkten är 3, -6, och lutningen är 2, har vi ekvationen y+6 = 2(x-3).
Och förenkling, 2x — y = 12.
Om du löser två av de tre ekvationerna kommer värdena för x och y att hittas. För detta exempel:
Värdet av x = 8,05263;
Värdet av y = 4,10526.
Som i detta fall är koordinaterna för det sökta Ortcentrum.