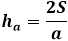Височина на триъгълник
В произволен триъгълник (където всички страни са с различни дължини), височини, начертани към страните , медиани и бисектриси представляват напълно различни линии. За да намерите височината в триъгълник, не можете да използвате свойствата на медианата или бисектрисата, както при равнобедрените или равностранните триъгълници, затова трябва да се използват други методи.
Един от подобните методи включва използването на общ параметър на триъгълника - площта. Алгоритъмът за изчисление се основава на факта, че площта на разностранен триъгълник може да бъде намерена по няколко начина, включително чрез височината. Знаейки трите страни на триъгълника, можете да намерите неговата площ, използвайки формулата на Херон, и след това, използвайки друга формула за площ, да изразите височината чрез нея.
За да изчислите площта на триъгълник, използвайки формулата на Херон, първо трябва да изчислите полупериметъра на триъгълника. Както подсказва името, полупериметърът е периметърът, или сумата от дължините на всичките три страни, разделен на две.
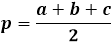
Самата формула за площ е произведението на полупериметъра с неговата разлика от всяка страна, като цялото изразяване е под квадратен корен.
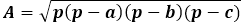
От друга страна, същата площ на триъгълника чрез височината е равна на половината от произведението на страната на триъгълника с височината, спусната към нея. Така, височината е равна на два пъти площта, разделена на страната на триъгълника. От предходната формула можете да изразите площта чрез трите страни на триъгълника и да я заместите във формулата за височина.
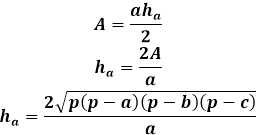
Тази формула за височина чрез страните на триъгълника е приложима за всякакви триъгълници, разностранни, равнобедрени или равностранни, при липса на други.
Изчисляването на височината на триъгълник, знаейки трите страни, изисква дълъг път, използвайки формулите за площ. Височината на триъгълника, изразена чрез площта, е свързана само със страната, на която е спусната, затова е изключително важно правилно да се посочи редът на страните за калкулатора и при ръчно изчисление да се замести съответната страна във формулата за височина.
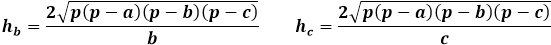
Формула за височина на произволен триъгълник чрез площта