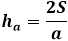Výška trojúhelníku

V libovolném trojúhelníku (kde všechny strany mají různou délku), výšky kreslené ke stranám , střední čáry a bisektory představují zcela odlišné čáry. K nalezení výšky v trojúhelníku nelze použít vlastnosti střední čáry nebo bisektory jako u rovnoramenných nebo rovnostranných trojúhelníků, proto je nutné použít jiné metody.

Jedna z podobných metod zahrnuje použití obecného parametru trojúhelníku - plochy. Algoritmus výpočtu je založen na skutečnosti, že plochu různoramenného trojúhelníku lze nalézt několika způsoby, včetně přes výšku. Znát tři strany trojúhelníku, můžete najít jeho plochu pomocí Heronova vzorce, a poté pomocí jiného vzorce pro plochu vyjádřit výšku přes ni.

Pro výpočet plochy trojúhelníku pomocí Heronova vzorce nejprve potřebujete vypočítat poloviční obvod trojúhelníku. Jak název napovídá, poloviční obvod je obvod, nebo součet délek všech tří stran, dělený dvěma.

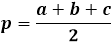
Vzorec pro plochu samotný je součinem polovičního obvodu s jeho rozdílem od každé strany, celý výraz je pod druhou odmocninou.

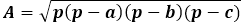
Na druhou stranu, stejná plocha trojúhelníku přes výšku je rovna polovině součinu strany trojúhelníku s výškou na ni spuštěnou. Takže výška je rovna dvojnásobku plochy dělené stranou trojúhelníku. Z předchozího vzorce můžete vyjádřit plochu přes tři strany trojúhelníku a nahradit ji ve vzorci pro výšku.

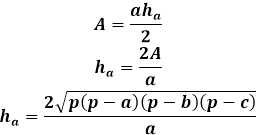
Tento vzorec pro výšku přes strany trojúhelníku je použitelný pro jakékoli trojúhelníky, různoramenné, rovnoramenné nebo rovnostranné, pokud nejsou k dispozici jiné.

Výpočet výšky trojúhelníku znát tři strany vyžaduje dlouhou cestu používání vzorců pro plochu. Výška trojúhelníku vyjádřená přes plochu je pouze ve vztahu ke straně, na kterou je spuštěna, takže je velmi důležité správně označit pořadí stran pro kalkulačku a při ručním výpočtu nahradit odpovídající stranu ve vzorci pro výšku.

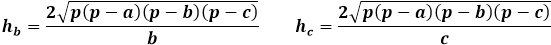
Vzorec výšky libovolného trojúhelníku přes plochu