Matrixtransponering

En transponeret matrix opnås ved at erstatte rækkerne i den oprindelige matrix med kolonner eller dens kolonner med rækker.

Egenskaber ved matrixtransponering:
En matrix transponeret to gange er lig med den oprindelige matrixA^TT(A^T)^T=A
Den transponerede matrix af en sum er lig med summen af de transponerede matricer(A + B)^T=A^T+B^T
Den transponerede matrix af et produkt er lig med produktet af de transponerede matricer af faktorerne, taget i omvendt rækkefølge(A × B)^T=A^T×B^T

For at opnå en transponeret matrix skal du udføre en af følgende handlinger med den oprindelige matrix:

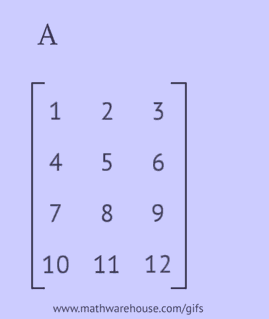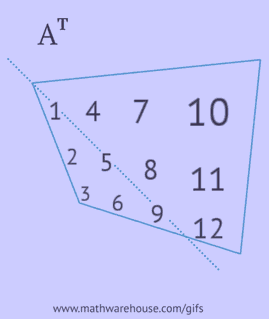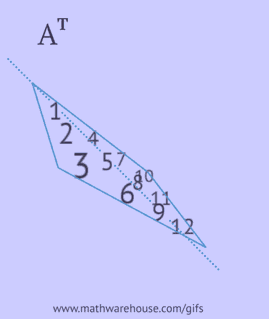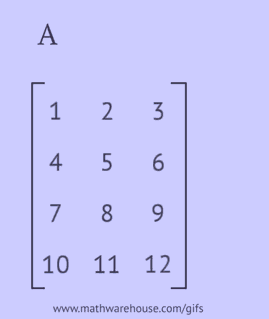
- skriv hver af dens rækker som en kolonne i samme rækkefølge;
- skriv hver af dens kolonner som en række i samme rækkefølge;
- reflekter dens elementer i forhold til hoveddiagonalen, startende fra det øverste venstre hjørne og fortsætte til højre og nedad, indtil den nederste eller højre kant nås.

Matricer omdannet til transponerede bruges til løsning af systemer af algebraiske ligninger, finde den inverse matrix, samt i andre opgaver inden for lineær algebra.