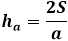Trekantshøjde

I en vilkårlig trekant (hvor alle sider har forskellige længder), højder tegnet til siderne , medianer og bisektorer repræsenterer helt forskellige linjer. For at finde højden i en trekant, kan du ikke bruge egenskaberne for medianen eller bisektoren som for ligebenede eller ligesidede trekanter, så andre metoder skal bruges.

En af de lignende metoder involverer brugen af en fælles parameter for trekanten - arealet. Beregningens algoritme er baseret på, at arealet af en vilkårlig trekant kan findes på flere måder, herunder gennem højden. Ved at kende de tre sider af trekanten, kan du finde dens areal ved hjælp af Herons formel, og derefter ved hjælp af en anden arealformel, udtrykke højden gennem den.

For at beregne arealet af en trekant ved hjælp af Herons formel, skal du først beregne halvperimeteren af trekanten. Som navnet antyder, er halvperimeteren omkredsen, eller summen af længderne af alle tre sider, divideret med to.

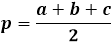
Selve arealformlen er produktet af halvperimeteren med dens forskel fra hver side, hele udtrykket under kvadratroden.

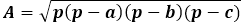
På den anden side er det samme areal af trekanten gennem højden lig med halvdelen af produktet af trekantens side med højden tegnet til den. Således er højden lig med to gange arealet divideret med trekantens side. Fra den tidligere formel kan du udtrykke arealet gennem de tre sider af trekanten og erstatte det i højdeformenten.

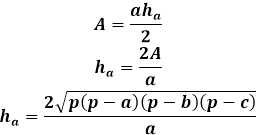
Denne højdeformel gennem trekantens sider er anvendelig for alle trekanter, vilkårlige, ligebenede eller ligesidede, i fraværet af andre.

Beregning af højden af en trekant ved at kende de tre sider kræver en lang vej ved hjælp af arealformler. Højden af trekanten udtrykt gennem arealet er kun relateret til den side, den er tegnet på, så det er ekstremt vigtigt at angive rækkefølgen af siderne korrekt for lommeregneren og i manuel beregning for at erstatte den passende side i højdeformenten.

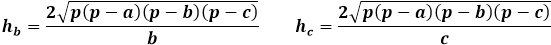
Højdeformel for en vilkårlig trekant gennem arealet