Orthozentrum — Schnittpunkt der Höhen des Dreiecks

Um das Orthozentrum eines Dreiecks zu finden, können Sie den Rechner verwenden, bei dem Sie die Koordinaten eingeben sollten. Im Automatikmodus werden die Berechnungen mit Formeln durchgeführt. Sie können auch alle Berechnungen manuell durchführen.

Zum Beispiel sind folgende Datenpunkte verfügbar:
A – 4,3;
In – 0,5;
Mit – 3,-6.
Das Erste, was zu finden ist, ist die Steigung der Seiten, die mit - bezeichnet wird m , unter Verwendung der Formel:

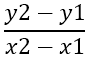
Daraus folgt:

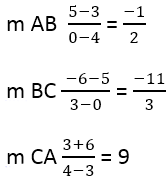
Als nächstes ist es notwendig, die Steigung der senkrechten Seiten zu finden, hierfür wird die Formel verwendet:

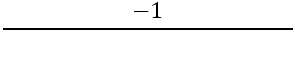
Wir haben:
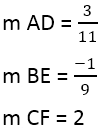Wenn die Steigung der Senkrechten gefunden ist, können Sie die Gleichung der Linien verwenden, zum Beispiel für die Linie AD, wo der Punkt 4,3 ist und die Steigung 3/11:

Mit Hilfe der Vereinfachung haben wir: 3x - 11y=-21
Für die Linie VE, wo der Punkt 0,5 ist und die Steigung -1/9, haben wir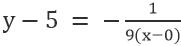

Vereinfachung ergibt: x+9y=45.
Und die letzten Linien CF, wo der Punkt 3, -6 ist und die Steigung 2, haben wir die Gleichung y+6 = 2(x-3).
Und Vereinfachung, 2x — y = 12.
Wenn Sie zwei der drei Gleichungen lösen, werden die Werte von x und y gefunden. Für dieses Beispiel:
Wert von x = 8,05263;
Wert von y = 4,10526.
Die in diesem Fall die Koordinaten des gesuchten Orthozentrums sind.