Ορθόκεντρο — σημείο διασταύρωσης των υψών του τριγώνου

Για να βρείτε το ορθόκεντρο ενός τριγώνου, μπορείτε να χρησιμοποιήσετε τον υπολογιστή όπου πρέπει να εισάγετε τις συντεταγμένες. Σε αυτόματη λειτουργία, οι υπολογισμοί θα εκτελούνται χρησιμοποιώντας φόρμουλες. Μπορείτε επίσης να εκτελέσετε όλους τους υπολογισμούς χειροκίνητα.

Για παράδειγμα, οι ακόλουθες δεδομένες είναι διαθέσιμες:
Α – 4,3;
Σε – 0,5;
Με – 3,-6.
Το πρώτο πράγμα που πρέπει να βρείτε είναι η κλίση των πλευρών, η οποία σημειώνεται με - m , χρησιμοποιώντας τον τύπο:

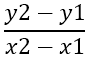
Από αυτό προκύπτει:

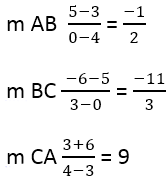
Στη συνέχεια, είναι απαραίτητο να βρείτε την κλίση των κάθετων πλευρών, για αυτό χρησιμοποιείται ο τύπος:

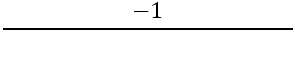
Έχουμε:
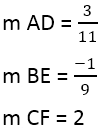Όταν βρεθεί η κλίση των κάθετων, μπορείτε να χρησιμοποιήσετε την εξίσωση των γραμμών, για παράδειγμα, για τη γραμμή AD, όπου το σημείο είναι 4,3, και η κλίση είναι 3/11:

Με τη βοήθεια απλοποίησης, έχουμε: 3x - 11y=-21
Για τη γραμμή VE, όπου το σημείο είναι 0,5, και η κλίση είναι -1/9, έχουμε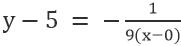

Η απλοποίηση δίνει: x+9y=45.
Και οι τελευταίες γραμμές CF, όπου το σημείο είναι 3, -6, και η κλίση είναι 2, έχουμε την εξίσωση y+6 = 2(x-3).
Και η απλοποίηση, 2x — y = 12.
Αν λύσετε δύο από τις τρεις εξισώσεις, θα βρεθούν οι τιμές των x και y. Για αυτό το παράδειγμα:
Τιμή του x = 8,05263;
Τιμή του y = 4,10526.
Οι οποίες σε αυτήν την περίπτωση είναι οι συντεταγμένες του αναζητούμενου ορθόκεντρου.