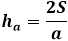Kolmnurga Kõrgus

Suvalises kolmnurgas (kus kõik küljed on erineva pikkusega), kõrgused tõmmatud külgedele , mediaanid ja bissektriksid esindavad täiesti erinevaid jooni. Kolmnurga kõrguse leidmiseks ei saa kasutada mediaani või bissektriksi omadusi nagu võrdhaarses või võrdkülgses kolmnurgas, seega tuleb kasutada teisi meetodeid.

Üks sarnastest meetoditest hõlmab kolmnurga ühise parameetri - pindala kasutamist. Arvutamise algoritm põhineb asjaolul, et kolmnurga pindala saab leida mitmel viisil, sealhulgas kõrguse abil. Teades kolmnurga kolme külge, saate leida selle pindala Heroni valemi abil, ja seejärel kasutades teist pindala valemit, väljendada kõrgust selle kaudu.

Et arvutada kolmnurga pindala Heroni valemi abil, peate esmalt arvutama kolmnurga poolümbermõõdu. Nagu nimi viitab, on poolümbermõõt ümbermõõt ehk kõigi kolme külje pikkuste summa, jagatud kahega.

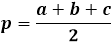
Pindala valem ise on poolümbermõõdu korrutis selle erinevusega igast küljest, kogu avaldis on ruutjuure all.

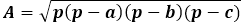
Teisest küljest on kolmnurga sama pindala kõrguse kaudu võrdne kolmnurga külje ja sellele langetatud kõrguse korrutise poolega. Seega on kõrgus võrdne pindala kahekordse jagatisega kolmnurga küljega. Eelmisest valemist saate väljendada pindala kolmnurga kolme külje kaudu ja asendada see kõrguse valemisse.

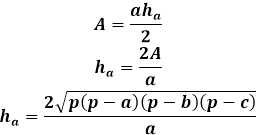
See kõrguse valem kolmnurga külgede kaudu kehtib iga kolmnurga puhul, olgu see võrdkülgne, võrdhaarne või suvaline, teiste puudumisel.

Kolmnurga kõrguse arvutamine teades kolme külge nõuab pikka teed pindala valemite kasutamise kaudu. Kolmnurga kõrgus, mis on väljendatud pindala kaudu, on seotud ainult küljega, millele see on langetatud, seega on äärmiselt oluline kalkulaatori ja käsitsi arvutamise jaoks õigesti külgede järjestus näidata, et asendada sobiv külg kõrguse valemisse.

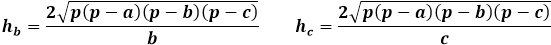
Suvalise kolmnurga kõrguse valem läbi pindala