Kolmio – on geometrinen kuvio, jolla on kolme pistettä, jotka eivät sijaitse samalla suoralla, ja kolme segmenttiä, jotka yhdistävät nämä pisteet pareittain. Kolmion pisteitä kutsutaan sen kärjiksi, ja segmenttejä – sen sivuiksi.
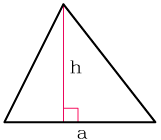
Verkkolaskimemme auttaa sinua laskemaan kolmion pinta-alan vain muutamassa sekunnissa. Tätä varten sinun on syötettävä tietyt tiedot, nimittäin sen pohjan pituus, jota edustaa latinalainen kirjain «a» ja kolmion korkeus, jota edustaa latinalainen kirjain «h». Kolmion pinta-ala lasketaan kaavalla: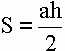osoittaa, että kolmion pinta-ala on yhtä suuri kuin sen pohjan pituuden ja korkeuden tulo jaettuna kahdella.
Kolmio – on geometrinen kuvio, jolla on kolme pistettä, jotka eivät sijaitse samalla suoralla, ja kolme segmenttiä, jotka yhdistävät nämä pisteet pareittain. Kolmion pisteitä kutsutaan sen kärjiksi, ja segmenttejä – sen sivuiksi.
osoittaa, että kolmion pinta-ala on yhtä suuri kuin sen pohjan pituuden ja korkeuden tulo jaettuna kahdella.