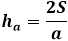Kolmion korkeus

Satunnaisessa kolmiossa (jossa kaikki sivut ovat eripituisia), korkeudet piirretty sivuille , keskilinjat ja kulmanpuolittajat edustavat täysin erilaisia viivoja. Kolmion korkeuden löytämiseksi ei voida käyttää keskilinjan tai kulmanpuolittajan ominaisuuksia kuten tasasivuisten tai yhteneväisten kolmioiden kohdalla, joten muita menetelmiä on käytettävä.

Yksi vastaavista menetelmistä käyttää kolmion yhteistä parametria - pinta-alaa. Laskenta-algoritmi perustuu siihen, että monikulmion kolmion pinta-ala voidaan löytää useilla tavoilla, mukaan lukien korkeuden kautta. Tietäen kolmion kolme sivua, voit löytää sen pinta-alan Heronin kaavan avulla, ja sitten toisen pinta-alan kaavan avulla ilmaista korkeus sen kautta.

Kolmion pinta-alan laskemiseksi Heronin kaavan avulla sinun on ensin laskettava kolmion puolipiiri. Nimensä mukaisesti puolipiiri on kolmion ympärysmitta eli kaikkien kolmen sivun pituuksien summa jaettuna kahdella.

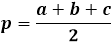
Pinta-alan kaava itsessään on puolipiirin tulo sen erotuksesta jokaisesta sivusta, koko ilmaisu neliöjuuren alla.

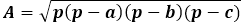
Toisaalta, sama kolmion pinta-ala korkeuden kautta on puolet kolmion sivun ja siihen pudotetun korkeuden tulosta. Näin ollen korkeus on kaksi kertaa pinta-ala jaettuna kolmion sivulla. Aiemmasta kaavasta voit ilmaista pinta-alan kolmion kolmen sivun kautta ja korvata sen korkeuden kaavassa.

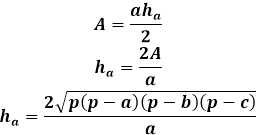
Tämä korkeuskaava kolmion sivujen kautta soveltuu kaikkiin kolmioihin, monikulmion, tasasivuiseen tai yhteneväiseen, muiden puuttuessa.

Kolmion korkeuden laskeminen tietäen kolme sivua vaatii pitkän reitin pinta-alan kaavojen avulla. Kolmion korkeus, joka on ilmaistu pinta-alan kautta, liittyy vain siihen sivuun, jolle se on pudotettu, joten on äärimmäisen tärkeää ilmoittaa sivujen järjestys oikein laskimelle ja manuaalisessa laskennassa korvataksesi oikean sivun korkeuden kaavaan.

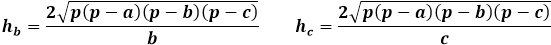
Satunnaisen kolmion korkeuskaava pinta-alan kautta