Transposition de matrice

Une matrice transposée est obtenue en remplaçant les lignes de la matrice d'origine par des colonnes ou ses colonnes par des lignes.

Propriétés de la transposition de matrice :
Une matrice transposée deux fois est égale à la matrice d'origine A^TT(A^T)^T=A
La matrice transposée d'une somme est égale à la somme des matrices transposées (A + B)^T=A^T+B^T
La matrice transposée d'un produit est égale au produit des matrices transposées des facteurs, prises dans l'ordre inverse (A × B)^T=A^T×B^T

Pour obtenir une matrice transposée, vous devez effectuer l'une des actions suivantes avec la matrice d'origine :

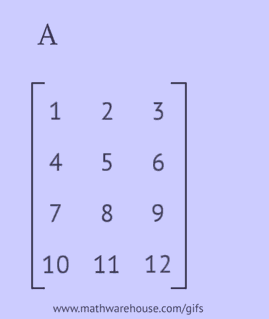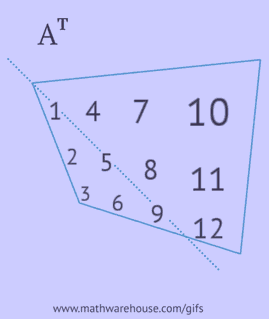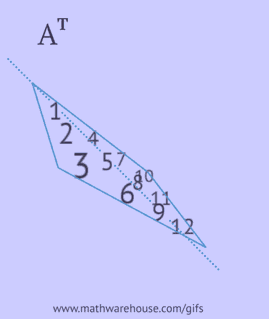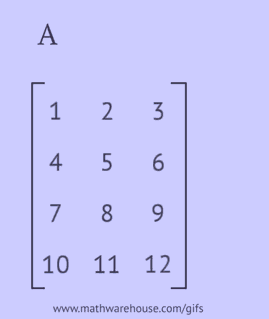
- écrire chacune de ses lignes comme une colonne dans le même ordre;
- écrire chacune de ses colonnes comme une ligne dans le même ordre;
- refléter ses éléments par rapport à la diagonale principale, en partant du coin supérieur gauche et en continuant vers la droite et vers le bas jusqu'à ce que le bord inférieur ou droit soit atteint.

Les matrices converties en transposées sont utilisées pour résoudre des systèmes d'équations algébriques, trouver la matrice inverse, ainsi que dans d'autres tâches de l'algèbre linéaire.