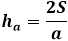Hauteur du triangle

Dans un triangle quelconque (où tous les côtés ont des longueurs différentes), les hauteurs tracées vers les côtés , médianes et bissectrices représentent des lignes complètement différentes. Pour trouver la hauteur dans un triangle, vous ne pouvez pas utiliser les propriétés de la médiane ou de la bissectrice comme pour les triangles isocèles ou équilatéraux, il faut donc utiliser d'autres méthodes.

L'une des méthodes similaires implique d'utiliser un paramètre commun du triangle - l'aire. L'algorithme de calcul repose sur le fait que l'aire d'un triangle quelconque peut être trouvée de plusieurs manières, y compris par la hauteur. En connaissant les trois côtés du triangle, vous pouvez trouver son aire en utilisant la formule de Héron, et ensuite en utilisant une autre formule d'aire, exprimer la hauteur à travers elle.

Pour calculer l'aire d'un triangle en utilisant la formule de Héron, vous devez d'abord calculer le demi-périmètre du triangle. Comme son nom l'indique, le demi-périmètre est le périmètre, ou la somme des longueurs des trois côtés, divisé par deux.

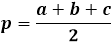
La formule de l'aire elle-même est le produit du demi-périmètre avec sa différence de chaque côté, l'ensemble de l'expression étant sous la racine carrée.

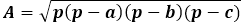
D'autre part, la même aire du triangle à travers la hauteur est égale à la moitié du produit du côté du triangle avec la hauteur tombée dessus. Ainsi, la hauteur est égale à deux fois l'aire divisée par le côté du triangle. À partir de la formule précédente, vous pouvez exprimer l'aire à travers les trois côtés du triangle et la remplacer dans la formule de la hauteur.

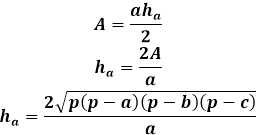
Cette formule de hauteur à travers les côtés du triangle est applicable pour tous les triangles, quelconques, isocèles ou équilatéraux, en l'absence d'autres.

Calculer la hauteur d'un triangle connaissant les trois côtés nécessite un long chemin utilisant des formules d'aire. La hauteur du triangle exprimée à travers l'aire n'est liée qu'au côté sur lequel elle est tombée, il est donc extrêmement important d'indiquer correctement l'ordre des côtés pour la calculatrice et dans le calcul manuel afin de substituer le côté approprié dans la formule de la hauteur.

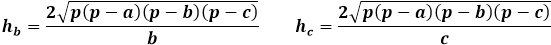
Formule de la hauteur d'un triangle quelconque à travers l'aire