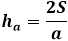Tinggi Segitiga

Dalam segitiga sembarang (di mana semua sisi memiliki panjang yang berbeda), tinggi yang ditarik ke sisi , median dan bisektor mewakili garis yang sepenuhnya berbeda. Untuk menemukan tinggi dalam segitiga, Anda tidak dapat menggunakan sifat median atau bisektor seperti pada segitiga sama kaki atau sama sisi, sehingga metode lain harus digunakan.

Salah satu metode yang serupa melibatkan penggunaan parameter umum dari segitiga - luas. Algoritma perhitungan didasarkan pada fakta bahwa luas segitiga sembarang dapat ditemukan dengan beberapa cara, termasuk melalui tingginya. Mengetahui ketiga sisi segitiga, Anda dapat menemukan luasnya menggunakan rumus Heron, dan kemudian menggunakan rumus luas lainnya, mengekspresikan tinggi melalui itu.

Untuk menghitung luas segitiga menggunakan rumus Heron, Anda pertama-tama perlu menghitung setengah keliling segitiga. Seperti namanya, setengah keliling adalah keliling, atau jumlah panjang ketiga sisi, dibagi dua.

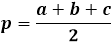
Rumus luas itu sendiri adalah hasil kali setengah keliling dengan selisihnya dari setiap sisi, seluruh ekspresi berada di bawah akar kuadrat.

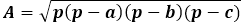
Di sisi lain, luas segitiga yang sama melalui tinggi sama dengan setengah hasil kali sisi segitiga dengan tinggi yang dijatuhkan ke sana. Dengan demikian, tinggi sama dengan dua kali luas dibagi dengan sisi segitiga. Dari rumus sebelumnya, Anda dapat mengekspresikan luas melalui ketiga sisi segitiga dan menggantinya dalam rumus tinggi.

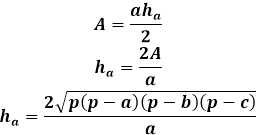
Rumus tinggi ini melalui sisi-sisi segitiga dapat diterapkan untuk segitiga apa pun, sembarang, sama kaki, atau sama sisi, jika tidak ada yang lain.

Menghitung tinggi segitiga mengetahui ketiga sisi memerlukan jalur panjang menggunakan rumus luas. Tinggi segitiga yang diekspresikan melalui luas hanya terkait dengan sisi tempat ia dijatuhkan, jadi sangat penting untuk menunjukkan urutan sisi secara tepat untuk kalkulator dan dalam perhitungan manual untuk menggantikan sisi yang sesuai dalam rumus tinggi.

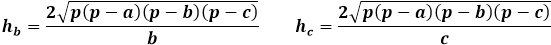
Rumus tinggi segitiga sembarang melalui luas