Trasposizione di matrice

Una matrice trasposta si ottiene sostituendo le righe della matrice originale con colonne o le sue colonne con righe.

Proprietà della trasposizione di matrice:
Una matrice trasposta due volte è uguale alla matrice originale A^TT(A^T)^T=A
La matrice trasposta di una somma è uguale alla somma delle matrici trasposte (A + B)^T=A^T+B^T
La matrice trasposta di un prodotto è uguale al prodotto delle matrici trasposte dei fattori, presi in ordine inverso (A × B)^T=A^T×B^T

Per ottenere una matrice trasposta, è necessario eseguire una delle seguenti azioni con la matrice originale:

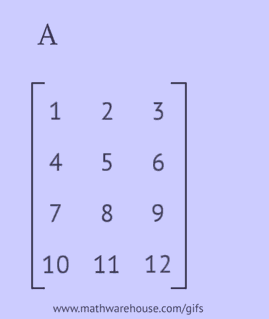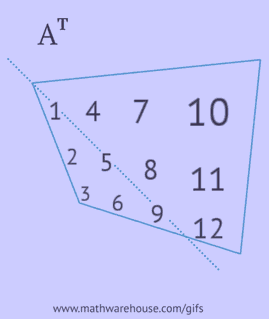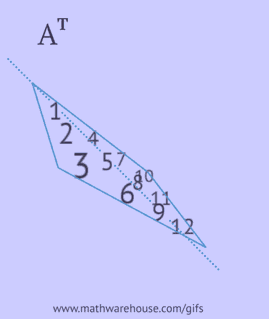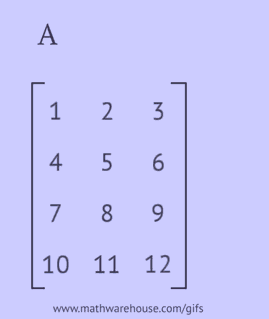
- scrivere ciascuna delle sue righe come una colonna nello stesso ordine;
- scrivere ciascuna delle sue colonne come una riga nello stesso ordine;
- riflettere i suoi elementi rispetto alla diagonale principale, partendo dall'angolo in alto a sinistra e continuando a destra e in basso fino a raggiungere il bordo inferiore o destro.

Le matrici convertite in trasposte sono utilizzate per risolvere sistemi di equazioni algebriche, trovare la matrice inversa, così come in altri compiti di algebra lineare.