行列の転置

転置行列は、元の行列の行を列に置き換えるか、列を行に置き換えることで得られます。

行列の転置の特性：
2回転置された行列は元の行列と等しいA^TT(A^T)^T=A
転置行列の和は転置行列の和と等しい(A + B)^T=A^T+B^T
積の転置行列は、逆順で取られた因数の転置行列の積と等しい(A × B)^T=A^T×B^T

転置行列を得るには、元の行列に対して次のアクションのいずれかを実行する必要があります：

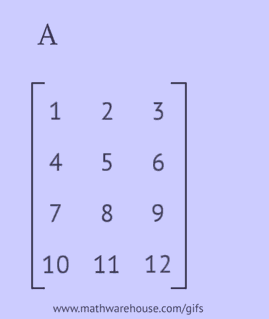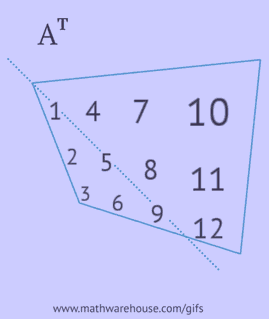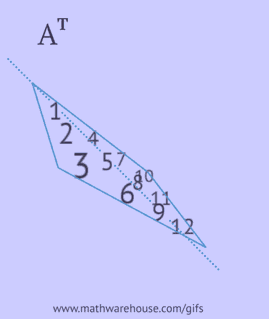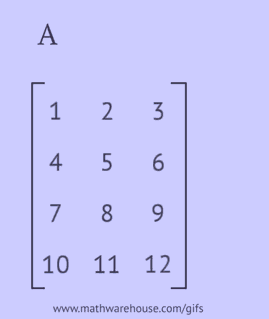
- 各行を同じ順序で列として書き込みます;
- 各列を同じ順序で行として書き込みます;
- 左上の角から始まり、右下または右の端に到達するまで、主対角線に沿ってその要素を反映します。

転置された行列は、代数方程式の解法、逆行列の発見、および線形代数の他のタスクで使用されます。