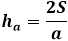三角形の高さ

任意の三角形で (すべての辺が異なる長さの場合) 、辺に引かれた高さ、 中線、 と 角の二等分線、 は完全に異なる線を表します。三角形の高さを見つけるには、二等辺三角形や正三角形のように中線や角の二等分線の特性を使用することはできないため、他の方法を使用する必要があります。

類似の方法の1つは、三角形の共通パラメータである面積を使用することを含みます。計算アルゴリズムは、スカレン三角形の面積を高さを通じて見つけることができるという事実に基づいています。三角形の三辺を知っていれば、その面積を見つけることができます ヘロンの公式を使用して面積を計算する, その後、別の面積公式を使用して、高さをそれに表現します。

ヘロンの公式を使用して三角形の面積を計算するには、まず三角形の半周を計算する必要があります。名前が示すように、半周は周囲、すなわち3つの辺の長さの合計を2で割ったものです。

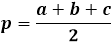
面積の公式自体は、半周と各辺からの差の積であり、全体が平方根の下にあります。

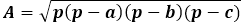
一方、三角形の同じ面積は、高さを通じて辺の半分の積に等しくなります。したがって、高さは面積を2倍して三角形の辺で割ったものに等しくなります。前の公式から、三角形の三辺を通じて面積を表現し、それを高さの公式に置き換えることができます。

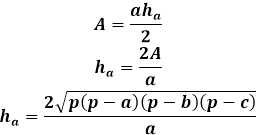
この高さの公式は、他のものがない場合、スカレン、二等辺、または正三角形のいずれにおいても適用可能です。

三角形の三辺を知っている高さを計算するには、面積の公式を使用して長い道のりを要します。面積を通じて表現された三角形の高さは、ドロップされた辺にのみ関連しているため、計算機と手動の計算で適切な順序で辺を指示し、高さの公式に適切な辺を代入することが非常に重要です。

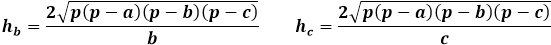
任意の三角形の面積を通じての高さの公式