Matricas transponēšana

Transponēta matrica tiek iegūta, aizstājot sākotnējās matricas rindas ar kolonnām vai tās kolonnas ar rindām.

Matricas transponēšanas īpašības:
Divreiz transponēta matrica ir vienāda ar sākotnējo matrica A^TT(A^T)^T=A
Transponēta summas matrica ir vienāda ar transponēto matricu summu (A + B)^T=A^T+B^T
Transponēta produkta matrica ir vienāda ar faktoru transponēto matricu reizinājumu, ņemot tos apgrieztā secībā (A × B)^T=A^T×B^T

Lai iegūtu transponētu matricu, jums jāveic viena no šādām darbībām ar sākotnējo matricu:

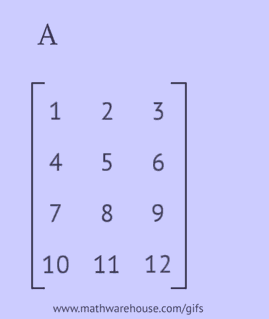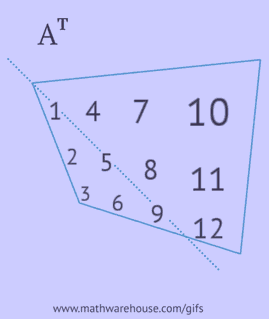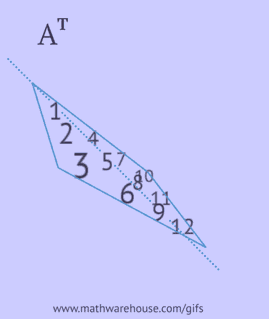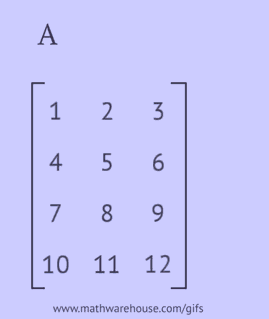
- uzrakstiet katru tās rindu kā kolonnu tajā pašā secībā;
- uzrakstiet katru tās kolonnu kā rindu tajā pašā secībā;
- atspoguļojiet tās elementus attiecībā pret galveno diagonāli, sākot no augšējā kreisā stūra un turpinot pa labi un uz leju, līdz sasniedz apakšējo vai labo malu.

Matricas, kas pārvērstas par transponētām, tiek izmantotas algebrisko vienādojumu sistēmu risināšanai, inversās matricas atrašanai, kā arī citos lineārās algebras uzdevumos.