Matrixtranspositie

Een getransponeerde matrix wordt verkregen door de rijen van de oorspronkelijke matrix te vervangen door kolommen of zijn kolommen door rijen.

Eigenschappen van matrixtranspositie:
Een matrix die tweemaal is getransponeerd, is gelijk aan de oorspronkelijke matrixA^TT(A^T)^T=A
De getransponeerde matrix van een som is gelijk aan de som van de getransponeerde matrices(A + B)^T=A^T+B^T
De getransponeerde matrix van een product is gelijk aan het product van de getransponeerde matrices van de factoren, in omgekeerde volgorde genomen(A × B)^T=A^T×B^T

Om een getransponeerde matrix te verkrijgen, moet je een van de volgende acties uitvoeren met de oorspronkelijke matrix:

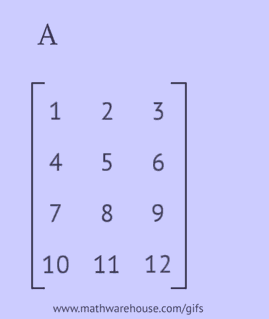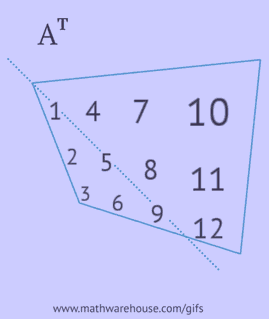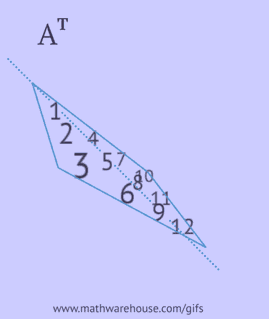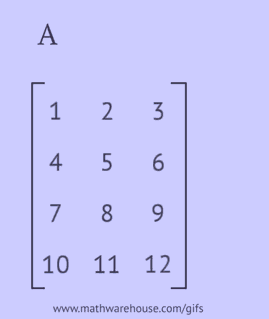
- schrijf elk van zijn rijen als een kolom in dezelfde volgorde;
- schrijf elk van zijn kolommen als een rij in dezelfde volgorde;
- reflecteer zijn elementen ten opzichte van de hoofddiagonaal, beginnend vanuit de linkerbovenhoek en ga verder naar rechts en naar beneden totdat de onderste of rechterrand is bereikt.

Matrices omgezet in getransponeerde worden gebruikt voor het oplossen van stelsels van algebraïsche vergelijkingen, het vinden van de inverse matrix, evenals in andere taken van lineaire algebra.