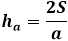Driehoek Hoogte

In een willekeurige driehoek (waar alle zijden verschillende lengtes hebben), hoogtes getekend naar de zijden , mediaan en bissectrices vertegenwoordigen compleet verschillende lijnen. Om de hoogte in een driehoek te vinden, kunt u de eigenschappen van de mediaan of bissectrice niet gebruiken zoals bij gelijkbenige of gelijkzijdige driehoeken, dus moeten andere methoden worden gebruikt.

Een van de vergelijkbare methoden houdt in dat een gemeenschappelijke parameter van de driehoek, de oppervlakte, wordt gebruikt. Het berekeningsalgoritme is gebaseerd op het feit dat de oppervlakte van een ongelijkzijdige driehoek op verschillende manieren kan worden gevonden, waaronder via de hoogte. Wetende de drie zijden van de driehoek, kunt u zijn oppervlakte vinden met de formule van Heron, en vervolgens met een andere oppervlakteformule de hoogte uitdrukken.

Om de oppervlakte van een driehoek te berekenen met de formule van Heron, moet u eerst de halve omtrek van de driehoek berekenen. Zoals de naam al aangeeft, is de halve omtrek de omtrek, of de som van de lengtes van alle drie de zijden, gedeeld door twee.

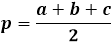
De oppervlakteformule zelf is het product van de halve omtrek met het verschil ervan van elke zijde, de hele uitdrukking onder de vierkantswortel.

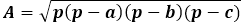
Aan de andere kant is dezelfde oppervlakte van de driehoek via de hoogte gelijk aan de helft van het product van de zijde van de driehoek met de hoogte die daarop neergelaten is. Dus de hoogte is gelijk aan tweemaal de oppervlakte gedeeld door de zijde van de driehoek. Uit de vorige formule kunt u de oppervlakte uitdrukken via de drie zijden van de driehoek en deze vervangen in de hoogteformule.

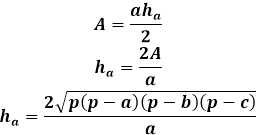
Deze hoogteformule via de zijden van de driehoek is toepasbaar voor elke driehoek, ongelijkzijdig, gelijkbenig of gelijkzijdig, bij afwezigheid van anderen.

Het berekenen van de hoogte van een driehoek met kennis van de drie zijden vereist een lange weg met gebruik van oppervlakteformules. De hoogte van de driehoek, uitgedrukt via de oppervlakte, is alleen gerelateerd aan de zijde waarop hij neergelaten wordt, dus het is uiterst belangrijk om de volgorde van de zijden correct aan te geven voor de calculator en bij handmatige berekening om de juiste zijde in de hoogteformule te vervangen.

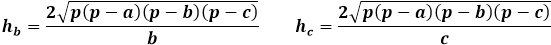
Hoogteformule van een willekeurige driehoek via de oppervlakte