Addisjon av Brøker
Addisjon av Brøker med Samme Nevnere:
Definisjon: Summen av brøker med samme nevnere kalles en brøk hvis teller er lik summen av tellerne i de opprinnelige brøkene, med en nevner lik nevneren til begge brøkene.Formel
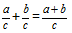
La oss legge til to brøker med samme nevnere
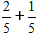
I henhold til formelen legger vi til tellerne, og beholder nevneren den samme
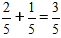
Viktig: Hvis mulig, skriver vi den forenklede brøken i det endelige svaret.
Eksempel:
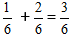Når vi forenkler brøken, får vi tallet 1/2 Addisjon av Brøker med Ulike Nevnere:
Definisjon: For å finne summen av brøker med ulike nevnere, bring først brøkene til en felles nevner, og legg dem deretter til som brøker med samme nevnere.Oppgave:
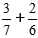
Løsningsprosess:
1) Vi bringer brøkene til en felles nevner.
For å gjøre dette, finner vi NOK - Minste Felles Multiplum, for nevnere 7 og 6, er dette tallet 42.
Del tallet 42 med nevnerne til brøkene 3/7 og 2/6
Slik fant vi de ekstra multiplikatorene.
Deretter multipliserer vi brøkene med de ekstra multiplikatorene og får uttrykket:
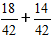
2) Legg til brøkene.
I vårt tilfelle kan brøken forenkles med 2, og i det endelige svaret skriver vi tallet 16/21
Addisjon av en Brøk og et Heltall:
Definisjon: For å legge til en brøk til et heltall, representer først hele tallet som en brøk med en nevner lik 1.Beregningens Algoritme:
1) Vi bringer brøkene til en felles nevner.
2) Legg til brøkene
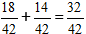
3) Hvis mulig, forenkle den resulterende brøken.
4) Hvis resultatet er en uekte brøk, beregn hele delen fra den.
Eksempel:
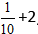
Løsning:
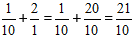
Beregne den hele delen, og få svaret
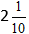
Addisjon av Blandet Brøk:
Definisjon: For å legge til blandede brøker må du legge til hele delene separat, og legge til brøkdelene separat.Formel
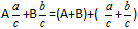
Eksempel:
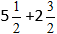
Sett tallene inn i formelen:
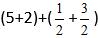
Vi får:
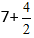
Fra brøken, beregn hele delen da den er uekte, og få uttrykket 7+2=9.