• All calculators
    • /
  • Education and science
    • /
  • Mathematics
    • /   Orthocenter — intersection point of the heights of the triangle

    Orthocenter — intersection point of the heights of the triangle

    To find the orthocenter of a triangle, you can use the calculator where you should enter the coordinates. In automatic mode, calculations will be performed using formulas. You can also perform all calculations manually.

    Point Coordinates X Coordinates Y
    A
    B
    C
    Orthocenter of a Triangle

    For example, the following data points are available:
    A – 4,3;
    In – 0,5;
    With – 3,-6.
     The first thing to find is the slope of the sides, which is denoted by - m , using the formula:

    Orthocenter formula—intersection point of altitudes of a triangle

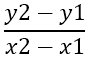
    From this it follows:
    Orthocenter formula—intersection point of altitudes of a triangle

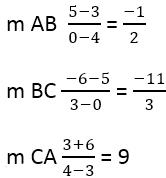
    Next, it is necessary to find the slope of the perpendicular sides, for this the formula is used:

    Orthocenter formula—intersection point of altitudes of a triangle

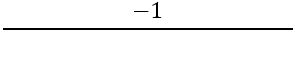
    We have:
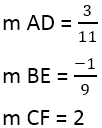    Orthocenter formula—intersection point of altitudes of a triangle When the slope of the perpendiculars is found, you can use the equation of lines, for example, for the line AD, where the point is 4,3, and the slope is 3/11:

    y-y1 = m(x-x1) y-3 = 3/11(x-4)

    With the help of simplification, we have: 3x - 11y=-21
    For the line VE, where the point is 0,5, and the slope is -1/9, we have 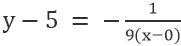Orthocenter formula—intersection point of altitudes of a triangle

    Simplification gives: x+9y=45.
    And the last lines CF, where the point is 3, -6, and the slope is 2, we have the equation y+6 = 2(x-3).
    And simplification, 2x — y = 12.
    If you solve two of the three equations, the values of x and y will be found. For this example:
    Value of x = 8,05263;
    Value of y = 4,10526.
    Which in this case are the coordinates of the sought Orthocenter.