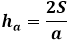Triangle Height
In an arbitrary triangle (where all sides are of different lengths), heights drawn to the sides , medians and bisectors represent completely different lines. To find the height in a triangle, you cannot use the properties of the median or bisector as for isosceles or equilateral triangles, so other methods must be used.
One of the similar methods involves using a common parameter of the triangle - the area. The calculation algorithm is based on the fact that the area of a scalene triangle can be found in several ways, including through the height. Knowing the three sides of the triangle, you can find its area using Heron's formula, and then using another area formula, express the height through it.
To calculate the area of a triangle using Heron's formula, you first need to calculate the semi-perimeter of the triangle. As the name suggests, the semi-perimeter is the perimeter, or the sum of the lengths of all three sides, divided by two.
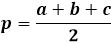
The area formula itself is the product of the semi-perimeter with its difference from each side, the entire expression being under the square root.
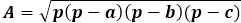
On the other hand, the same area of the triangle through the height equals half the product of the triangle's side with the height dropped to it. Thus, the height is equal to twice the area divided by the triangle's side. From the previous formula, you can express the area through the three sides of the triangle and replace it in the height formula.
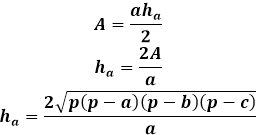
This height formula through the triangle's sides is applicable for any triangles, scalene, isosceles, or equilateral, in the absence of others.
Calculating the height of a triangle knowing the three sides requires a long path using area formulas. The height of the triangle expressed through the area is only related to the side it is dropped on, so it's extremely important to properly indicate the order of the sides for the calculator and in manual calculation to substitute the appropriate side into the height formula.
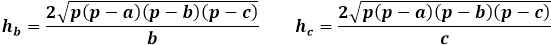
Height formula of an arbitrary triangle through the area