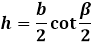Isosceles Triangle Height
An isosceles triangle is called a triangle where two of the three sides are equal to each other. The equal sides are considered the lateral sides a, and the third side b is called the base of the isosceles triangle.
Accordingly, in such a triangle, you can draw three heights, two of which will be equal to each other, similar to the sides - these are the heights dropped to the lateral side of the triangle a, and the third height is dropped to the base. The height of the triangle is drawn from the angle of the triangle to the opposite side at a right angle. Most problems with the height of a triangle are solved through the right triangles it forms.
Let's consider each case separately.
The height of an isosceles triangle, dropped to the base, has a number of individual properties unique to it and not applicable to other heights in such a triangle. In particular, the height drawn to the base of the isosceles triangle coincides with the median and bisector, drawn to the base, therefore, it not only forms a right angle with the base but also divides it into two equal parts, like a median, and similarly divides the angle in half, like a bisector. As a result, the height is a kind of axis of symmetry of the triangle and divides it into two congruent right triangles. In such a triangle, the height is a leg, and to find its length, it is necessary to relate the sides of the isosceles triangle to the sides of the right triangle. The lateral side of the isosceles triangle becomes the hypotenuse, and to determine the second leg, the base of the isosceles triangle must be divided in half, by the property of the median.
The length of the height of an isosceles triangle is equal by Pythagorean theorem to the square root of the sum of the square of the lateral side of the isosceles triangle and a quarter of the square of the base of the isosceles triangle:
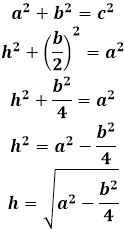
The second case, when the conditions of the problem require finding the height dropped to the lateral side of the isosceles triangle, is revealed most simply through the area of the triangle.
The area of any triangle can be found in several ways - for example, through the three sides of the triangle using Heron's formula, or through the height, multiplying it by half the side to which it is dropped. Both methods yield identical area values, so both formulas can be equated and from there derive the final formula for the height dropped to the lateral side of the isosceles triangle.
Heron's formula for an isosceles triangle will have a somewhat simplified form due to the repetition of the values of the lateral sides:
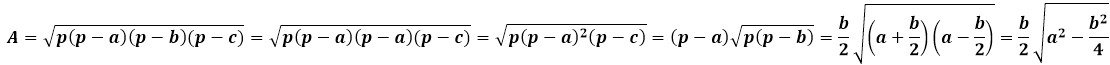
Isosceles Triangle Area through the height dropped to the lateral side

The same formula can be used to find any height in an isosceles triangle if the corresponding sides are swapped in the formula.
Height formula of an isosceles triangle through the lateral side and angle at the base α: h=a sinα
Formula through the lateral side and angle opposite the base β:
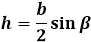
Formula through the base and angle at it α:
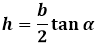
through the base and angle opposite it β: