Transpozycja macierzy

Macierz transponowana jest uzyskiwana przez zamianę wierszy oryginalnej macierzy na kolumny lub jej kolumn na wiersze.

Właściwości transpozycji macierzy:
Macierz transponowana dwukrotnie jest równa oryginalnej macierzy A^TT(A^T)^T=A
Transponowana macierz sumy jest równa sumie macierzy transponowanych (A + B)^T=A^T+B^T
Transponowana macierz iloczynu jest równa iloczynowi macierzy transponowanych czynników, wziętych w odwrotnej kolejności (A × B)^T=A^T×B^T

Aby uzyskać macierz transponowaną, należy wykonać jedną z następujących czynności z oryginalną macierzą:

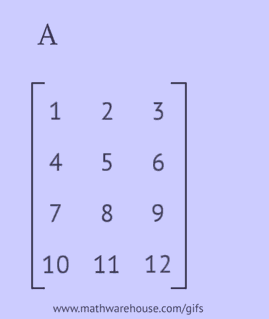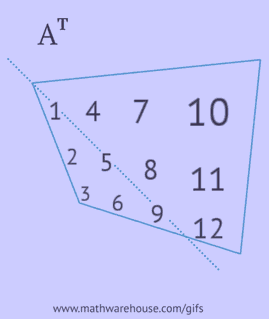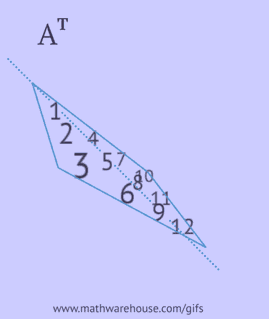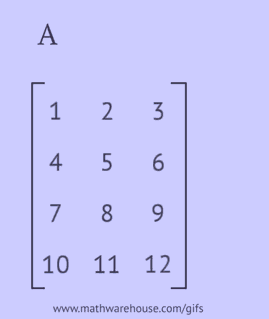
- zapisz każdy z jej wierszy jako kolumnę w tej samej kolejności;
- zapisz każdą z jej kolumn jako wiersz w tej samej kolejności;
- odzwierciedlić jej elementy względem głównej przekątnej, zaczynając od lewego górnego rogu i kontynuując w prawo i w dół, aż osiągnie dolną lub prawą krawędź.

Macierze przekształcone na transponowane są używane do rozwiązywania układów równań algebraicznych, znajdowania macierzy odwrotnej oraz w innych zadaniach algebry liniowej.